[1] 193.5 402.5方法論特殊講義III
マッチング
関西大学総合情報学部
2025-08-18
マッチングの考え方
因果推論と内生性
内生性: 処置変数と誤差項間の相関関係
- 内生性は因果推論の敵
- 例
- 処置変数 = ソンさんの講義を履修するか否か
- 結果変数 = 10年後の年収
- もし、やる気のある学生が履修する傾向があるとしたら?
- やる気のある学生は履修の有無と関係なく、高所得者になりやすい。
- \(\rightarrow\) 「やる気」は処置と結果、両方と連関している
RCTの限界
- 高費用
- 数万〜数億円
- 倫理的な問題による実行不可能性
- 喫煙と健康
- Philip Zimbardo. 2008. The Lucifer Effect: How Good People Turn Evil. Rider.
- 外的妥当性の問題
- Michael G. Findley, Kyosuke Kikuta, and Michael Denly. 2021. “External Validity,” Annual Review of Political Science, 24:365-393.
- 回顧的因果推論には不向き
- 主に介入 (intervention)の効果が推定対象
観察データを用いた因果推論
もし、\(X\)をしたら(did)\(Y\)はどうなった(would)だろうか
- 過去を対象にRCTを行うことは不可能
- 過去に収集された観察データを使用した因果推論が必要
- マッチング、回帰不連続デザイン、差分の差分法、操作変数法など
割当メカニズム (assignment mechanism)
- ユニットが処置を受けるか否かを規定するメカニズム
- 例) 「やる気」が「履修」を規定
- 無作為割当なら無作為に処置を受けるか否かが決まるため、考える必要がない。
内生性への対処
matching_data1.csvの例(架空データ; 30行 \(\times\) 4列)
- 明らかに「やる気」と「履修」は連関
- 履修有無による平均年収の差は約265.333万円
# A tibble: 10 × 4
ID Income Yaruki Rishu
<dbl> <dbl> <dbl> <dbl>
1 1 659 0 1
2 2 587 1 1
3 3 628 1 1
4 4 563 1 1
5 5 531 1 1
6 6 79 0 0
7 7 356 0 1
8 8 176 0 0
9 9 339 0 0
10 10 520 1 1# A tibble: 10 × 4
ID Income Yaruki Rishu
<dbl> <dbl> <dbl> <dbl>
1 11 239 0 0
2 12 276 1 0
3 13 609 1 1
4 14 254 0 0
5 15 423 0 1
6 16 172 0 1
7 17 20 0 0
8 18 447 1 0
9 19 498 1 1
10 20 648 1 1# A tibble: 10 × 4
ID Income Yaruki Rishu
<dbl> <dbl> <dbl> <dbl>
1 21 155 0 0
2 22 768 1 1
3 23 463 1 0
4 24 309 1 0
5 25 304 0 0
6 26 408 1 1
7 27 259 0 0
8 28 516 1 1
9 29 476 1 0
10 30 110 0 0内生性への対処
方法:処置変数と結果変数に影響を与える要因(交絡要因)を揃える
- 「やる気」のない学生(
Yaruki == 0)だけに絞ってみる - 履修有無による平均年収の差は209万円
内生性への対処
方法: 処置変数と結果変数に影響を与える要因(交絡要因)を揃える
- 「やる気」のある学生(
Yaruki == 1)だけに絞ってみる - 履修有無による平均年収の差は176.3万円
[1] 394.2000 570.5455| ID | 所得 | やる気 | 履修 | ID | 所得 | やる気 | 履修 | |
|---|---|---|---|---|---|---|---|---|
| 2 | 587 | 1 | 1 | 12 | 276 | 1 | 0 | |
| 3 | 628 | 1 | 1 | 18 | 447 | 1 | 0 | |
| 4 | 563 | 1 | 1 | 23 | 463 | 1 | 0 | |
| 5 | 531 | 1 | 1 | 24 | 309 | 1 | 0 | |
| 10 | 520 | 1 | 1 | 29 | 476 | 1 | 0 | |
| 13 | 609 | 1 | 1 | |||||
| 19 | 498 | 1 | 1 | |||||
| 20 | 648 | 1 | 1 | |||||
| 22 | 768 | 1 | 1 | |||||
| 26 | 408 | 1 | 1 | |||||
| 28 | 516 | 1 | 1 | |||||
| Mean | 570.5 | Mean | 394.2 |
内生性への対処
| 履修 (T) | 平均年収 (Y) |
|---|---|
| 1 | 402.5 |
| 0 | 193.5 |
| 履修 (T) | 平均年収 (Y) |
|---|---|
| 1 | 570.5 |
| 0 | 394.2 |
やる気のある(ない)被験者を一人の被験者として考える場合、差分はITEと解釈可能。
| ID (i) | N | やる気 (Zi) | Yi(Ti = 1) | Yi(Ti = 0) | ITEi |
|---|---|---|---|---|---|
| 1 | 14 | 0 | 402.5 | 193.5 | 209.0 |
| 2 | 16 | 1 | 570.5 | 394.2 | 176.3 |
- ITEの加重平均 \(\rightarrow\) 講義履修の因果効果 \(\rightarrow\) 約191.6万円
マッチングの考え方
割当メカニズムを想定し、交絡要因が同じユニット同士を比較
- 交絡要因: 処置変数と結果変数、両方と関係のある変数
- 以下の条件が満たされる場合、マッチングで因果効果の推定が可能
- 条件付き独立の仮定 (Conditional Independece Assumption; CIA)
- \(\{Y_i(T_i = 1),Y_i(T_i = 0)\} \perp T_i∣X_i\)
- \(T_i\) : 学生 \(i\) の履修有無、 \(X_i\) : 学生 \(i\) のやる気
- やる気(=交絡要因)が同じ場合、学生 \(i\) がソンさんの講義を履修するか否か(=処置変数)は彼(女)の将来収入(=結果変数)と関係なく決まる
- \(\rightarrow\) 処置変数を外生変数として扱うことが可能に
- CIAが満たされるためには、割当メカニズム上のすべての交絡要因が必要
条件付き独立の仮定とは
| ID (i) | Zi | Ti | Y0, i | Y1, i |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 0 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 0 | 0 |
| 8 | 0 | 1 | 0 | 1 |
| 9 | 1 | 0 | 1 | 1 |
| 10 | 1 | 0 | 1 | 0 |
| 11 | 1 | 0 | 0 | 1 |
| 12 | 1 | 1 | 1 | 1 |
| 13 | 1 | 1 | 1 | 1 |
| 14 | 1 | 1 | 0 | 1 |
| 15 | 1 | 1 | 0 | 1 |
| 16 | 1 | 1 | 0 | 1 |
| 17 | 1 | 1 | 1 | 1 |
| 18 | 1 | 1 | 1 | 0 |
| 19 | 1 | 1 | 1 | 0 |
| 20 | 1 | 1 | 1 | 0 |
| X | Y0 | Y1 |
|---|---|---|
| T = 0 | 0.429 | 0.429 |
| T = 1 | 0.538 | 0.538 |
- 処置効果は0.538 − 0.429 = 0.109
- もし、統制群と処置群が同質なら
- A = C、そしてB = Dのはず
- 処置群がもし統制群になっても、今の統制群と同じ
- \(\Rightarrow\) 交換可能性が成立せず

条件付き独立の仮定とは
| ID (i) | Zi | Ti | Y0, i | Y1, i |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 0 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 0 | 0 |
| 8 | 0 | 1 | 0 | 1 |
| 9 | 1 | 0 | 1 | 1 |
| 10 | 1 | 0 | 1 | 0 |
| 11 | 1 | 0 | 0 | 1 |
| 12 | 1 | 1 | 1 | 1 |
| 13 | 1 | 1 | 1 | 1 |
| 14 | 1 | 1 | 0 | 1 |
| 15 | 1 | 1 | 0 | 1 |
| 16 | 1 | 1 | 0 | 1 |
| 17 | 1 | 1 | 1 | 1 |
| 18 | 1 | 1 | 1 | 0 |
| 19 | 1 | 1 | 1 | 0 |
| 20 | 1 | 1 | 1 | 0 |
\(Z\) で条件づけた場合 ( \(Z = 0\) )
| X | Y0 | Y1 |
|---|---|---|
| T = 0 | 0.250 | 0.250 |
| T = 1 | 0.250 | 0.250 |
- 処置効果は0.250 − 0.250 = 0.000
- もし、統制群と処置群が同質なら
- A = C、そしてB = Dが成立
- \(\Rightarrow\) 交換可能性が成立

条件付き独立の仮定とは
| ID (i) | Zi | Ti | Y0, i | Y1, i |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 0 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 0 | 0 |
| 8 | 0 | 1 | 0 | 1 |
| 9 | 1 | 0 | 1 | 1 |
| 10 | 1 | 0 | 1 | 0 |
| 11 | 1 | 0 | 0 | 1 |
| 12 | 1 | 1 | 1 | 1 |
| 13 | 1 | 1 | 1 | 1 |
| 14 | 1 | 1 | 0 | 1 |
| 15 | 1 | 1 | 0 | 1 |
| 16 | 1 | 1 | 0 | 1 |
| 17 | 1 | 1 | 1 | 1 |
| 18 | 1 | 1 | 1 | 0 |
| 19 | 1 | 1 | 1 | 0 |
| 20 | 1 | 1 | 1 | 0 |
\(Z\) で条件づけた場合 ( \(Z = 1\) )
| X | Y0 | Y1 |
|---|---|---|
| T = 0 | 0.667 | 0.667 |
| T = 1 | 0.667 | 0.667 |
- 処置効果は0.667 − 0.667 = 0.000
- もし、統制群と処置群が同質なら
- A = C、そしてB = Dが成立
- \(\Rightarrow\) 交換可能性が成立

条件付き独立の仮定とは
| ID (i) | Zi | Ti | Y0, i | Y1, i |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 0 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 0 | 0 |
| 8 | 0 | 1 | 0 | 1 |
| 9 | 1 | 0 | 1 | 1 |
| 10 | 1 | 0 | 1 | 0 |
| 11 | 1 | 0 | 0 | 1 |
| 12 | 1 | 1 | 1 | 1 |
| 13 | 1 | 1 | 1 | 1 |
| 14 | 1 | 1 | 0 | 1 |
| 15 | 1 | 1 | 0 | 1 |
| 16 | 1 | 1 | 0 | 1 |
| 17 | 1 | 1 | 1 | 1 |
| 18 | 1 | 1 | 1 | 0 |
| 19 | 1 | 1 | 1 | 0 |
| 20 | 1 | 1 | 1 | 0 |
条件付き独立が成立するということは
- 交換可能性が成立
- 処置群を統制群に、統制群を処置群にしても同じ結果が得られること
重回帰分析との比較
重回帰分析における回帰係数の解釈
- 他の変数すべてが同じ場合、ある変数が1単位変化する時の応答変数の変化量
- マッチングと同じ?
重回帰分析とマッチングの結果が近似することも \(\bigcirc\)
- 参考)手計算マッチングの結果:約191.6万円
- 計算時に小数点を切り捨てたため誤差あり
重回帰分析との比較
実質的にマッチングと回帰分析は同じという見解も (Angrist and Pischke 2009)
- 具体的に言えば、回帰分析はマッチングの特殊な形態
- 強い仮定を置いたマッチング
- 回帰分析は \(Y = \beta_0 + \beta_1 X_1 + ... + \beta_k X_k\) の関数型を仮定 (parametric)
- 回帰分析において誤差項の平均値は必ず0を仮定 ( \(\mathbb{E}(\varepsilon|T, X) = 0\) )
- マッチングの場合、( \(\mathbb{E}(\varepsilon|T = 0, X) = \mathbb{E}(\varepsilon|T = 1, X)\) )
- 回帰分析はオーバーラップ条件を無視する
- マッチングされないケースでも、線形関数によって予測されてしまう
- マッチングはオーバーラップされないケースを分析から除外する
- 結論: 回帰分析より柔軟、拡張性がある
ATE, ATT, ATC
3種類の因果効果
- ATE (Average Treatment Effect): 平均処置効果
- ATT (ATE for the Treated): 処置群における平均処置効果
- 潜在結果: 処置群が処置を受けなかった場合の応答変数
- ATC (ATE for the Control): 統制群における平均処置効果
- 潜在結果: 統制群が処置を受けた場合の応答変数
因果効果は一般的に母集団ではなく、サンプルから推定されるため、「SATE/SATT/SATC」と呼ばれる場合も
他にもRIE (Retrospective Intervention Effect) なども (Samii et al. 2016)
RCTでは主にATEが推定対象(マッチングでは区分するケースが多い)
統計ソフトウェアによってはATTを因果効果の推定値として表示する場合もある。
ATT: 処置群における平均処置効果
- 処置群の潜在的結果を統制群から割り当てる。
- 処置群は \(Y_i(T_i = 1)\) が観察済みであり、潜在的結果は \(Y_i(T_i = 0)\)
- やる気のない学生の \(Y_i(T_i = 0)\) は193.5、ある学生は394.2
| ID (i) | Yarukii | Yi(Ti = 1) | Yi(Ti = 0) | ITEi |
|---|---|---|---|---|
| 1 | 0 | 659 | 193.5 | 465.5 |
| 2 | 1 | 587 | 394.2 | 192.8 |
| 3 | 1 | 628 | 394.2 | 233.8 |
| 4 | 1 | 563 | 394.2 | 168.8 |
| 5 | 1 | 531 | 394.2 | 136.8 |
| 7 | 0 | 356 | 193.5 | 162.5 |
| ... | ... | ... | ... | ... |
| 20 | 1 | 648 | 394.2 | 253.8 |
| 22 | 1 | 768 | 394.2 | 373.8 |
| 26 | 1 | 408 | 394.2 | 13.8 |
| 28 | 1 | 516 | 394.2 | 121.8 |
| 平均 | 185.1 |
ATC: 統制群における平均処置効果
- 統制群の潜在的結果を処置群から割り当てる。
- 統制群は \(Y_i(T_i = 0)\) が観察済みであり、潜在的結果は \(Y_i(T_i = 1)\)
- やる気のない学生の \(Y_i(T_i = 1)\) は402.5、ある学生は570.5
| ID (i) | Yarukii | Yi(Ti = 1) | Yi(Ti = 0) | ITEi |
|---|---|---|---|---|
| 6 | 0 | 402.5 | 79 | 323.5 |
| 8 | 0 | 402.5 | 176 | 226.5 |
| 9 | 0 | 402.5 | 339 | 63.5 |
| 11 | 0 | 402.5 | 239 | 163.5 |
| 12 | 1 | 570.5 | 276 | 294.5 |
| 14 | 0 | 402.5 | 254 | 148.5 |
| ... | ... | ... | ... | ... |
| 25 | 0 | 402.5 | 304 | 98.5 |
| 27 | 0 | 402.5 | 259 | 143.5 |
| 29 | 1 | 570.5 | 476 | 94.5 |
| 30 | 0 | 402.5 | 110 | 292.5 |
| 平均 | 198.1 |
ATE: 平均処置効果
- ATTとATCの加重平均
- 今回は処置群と統制群が15:15 \(\rightarrow\) 単純平均でOK
- \(\frac{1}{2}(185.1 + 198.1) = 191.6\)
- 手計算マッチングとと同じ結果
\[\text{ATE} = \frac{N_{\text{treated}}}{N_{\text{all}}} \text{ATT} + \frac{N_{\text{controlled}}}{N_{\text{all}}} \text{ATC}.\]
様々なマッチング手法
マッチングいろいろ
- Exact Matching
- Nearest-neighbor Matching
- k-nearest Neighbor Matching
- Caliper Matching (Radius Matching)
- Coarsened Exact Matching
- Propensity Score Matching
- Inverse Probability Weighting
- Ensemble Matching
Exact Matching
- 「正確マッチング」、「厳格なマッチング」などで訳される
- これまで見てきた方法が Exact Matching
- データ内の共変量 (交絡要因) が完全に一致するケース同士の比較
- 共変量が少数、かつ、名目or順序変数の場合、使用可
- 共変量が多数、または連続変数の場合は実質的に無理
- 次元の呪い or 次元爆発

Nearest-neighbor Matching
Nearest-neighbor Matching
- 「最近傍マッチング」と訳される。
- 共変量が連続変数、多次元の場合、「完全に一致」ケースはない場合がほとんど
- \(\rightarrow\) 「一致」ではなく、「最も似ている」ケース同士と比較
- 共変量を座標(超)平面に位置づけた場合、最も近いケースをマッチング
「近さ」の基準
- Manhattan Distance
- Standardized Euclidean Distance
- Mahalanobis Distance (\(\leftarrow\) 最もよく使われる基準)
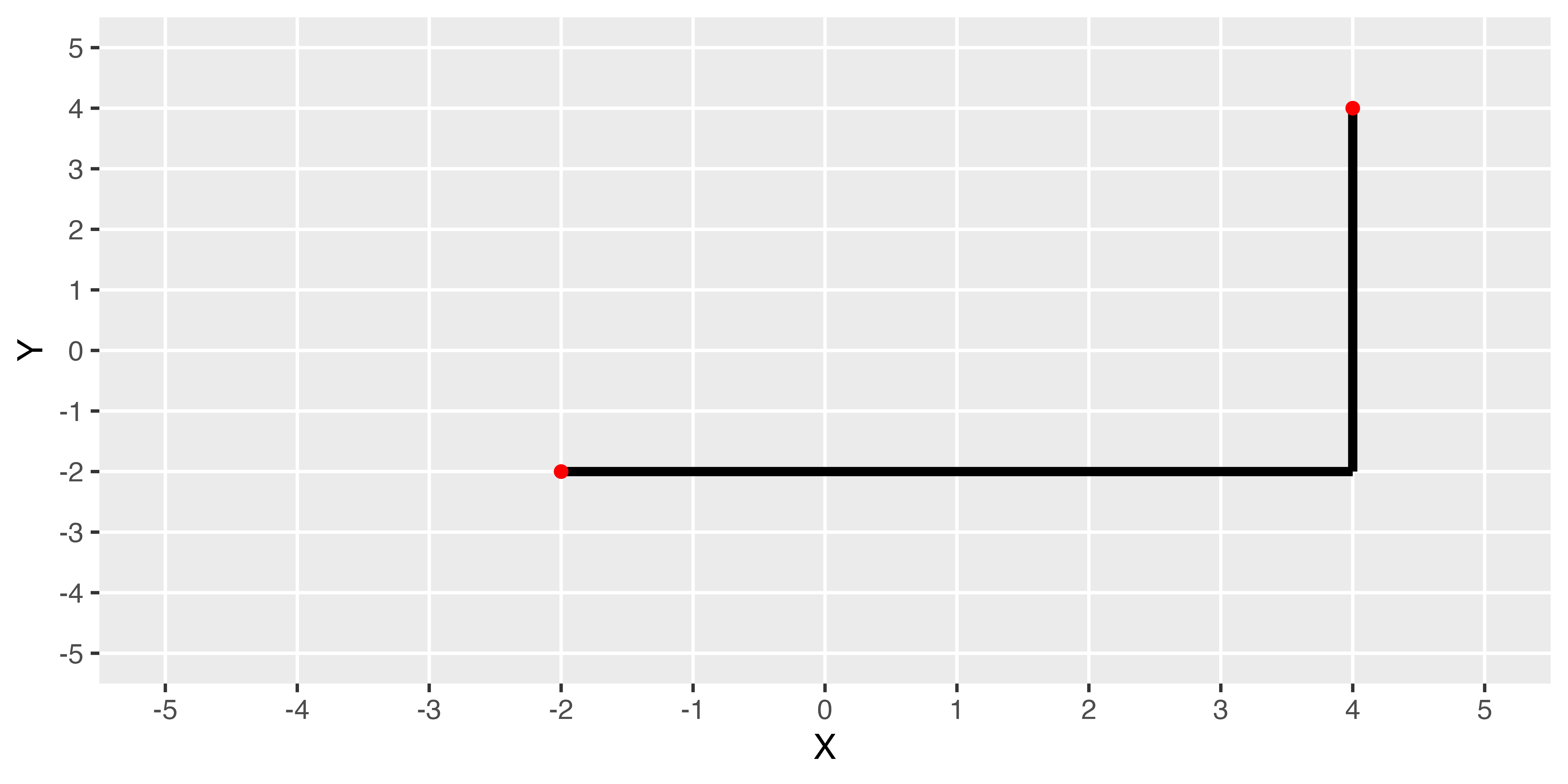
マンハッタン距離(Manhattan Distance; City-block Distance)
\[d(i, j) = |X_i - X_j| + |Y_i - Y_j| \text{ where } i \neq j.\]
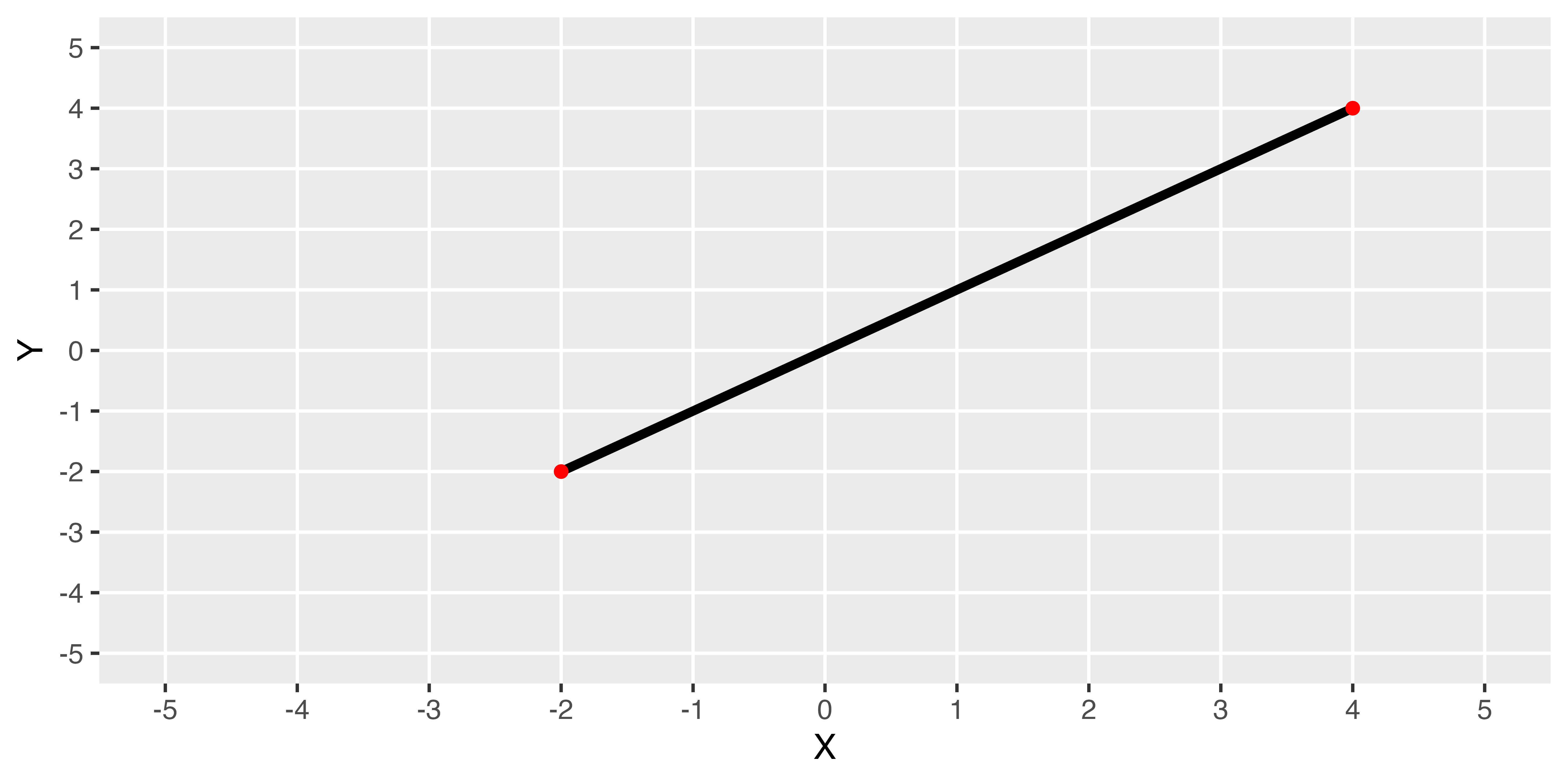
標準化ユークリッド距離(Standardized Euclidean Distance)
\[d(i, j) = \sqrt{\Bigg(\frac{X_i - X_j}{\sigma_X}\Bigg)^2 + \Bigg(\frac{Y_i - Y_j}{\sigma_Y}\Bigg)^2} \text{ where } i \neq j.\]

マハラノビス距離(Mahalanobis Distance)
- 共変量間の相関が0(\(\rho = 0\))の場合、Standardized Euclidean Distanceと同じ
\[d(i, j) = \sqrt{\frac{1}{1 - \rho^2_{X, Y}} \Bigg[\Bigg(\frac{X_i - X_j}{\sigma_X}\Bigg)^2 + \Bigg(\frac{Y_i - Y_j}{\sigma_Y}\Bigg)^2 - 2\rho_{X,Y}\Bigg(\frac{X_i - X_j}{\sigma_X}\Bigg) \Bigg(\frac{Y_i - Y_j}{\sigma_Y}\Bigg)\Bigg]} \text{ where } i \neq j.\]

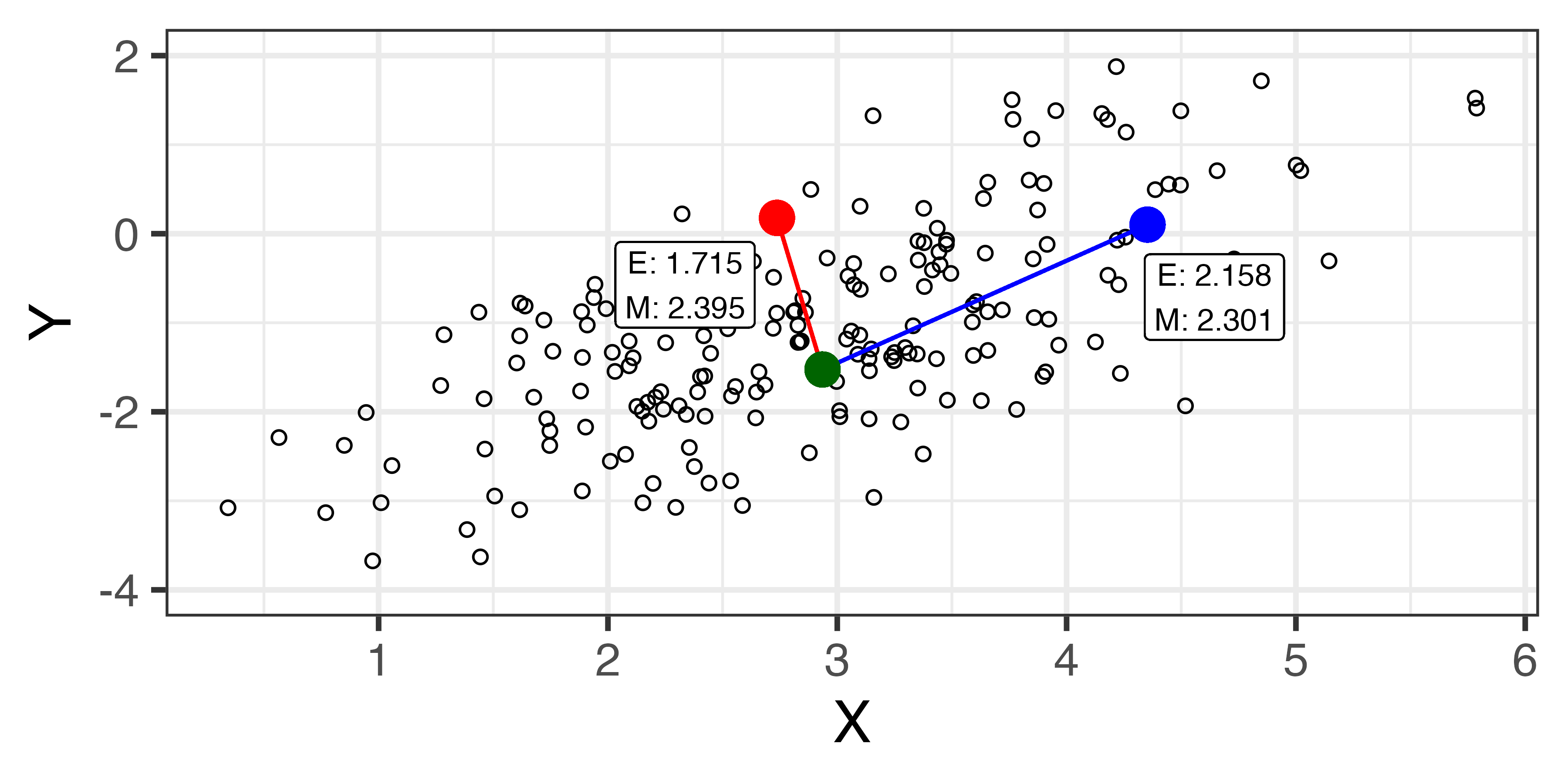
マッチング方法
ATTの場合、処置群のケースに統制群の中で最も近いケース1個を割当
- 近さの測定はマハラノビス距離が一般的
- 処置群内の1ケースに複数の統制群ケースを割り当てる場合も
- k-nearest Neighbor Matching
- Caliper Matching
- 復元マッチングと非復元マッチング
k-nearest Neighbor Matching
k-最近傍マッチング
- 最も近い1個ケースを潜在的結果として使うのではなく、最も近い \(k\) 個のケースの平均値を潜在的結果として用いる。
- \(j(m)\) : \(i\) から \(m\) 番目に近いケース \(j\)
\[Y_i(T_i = 0) = \begin{cases}Y_i & \text{ if } T_i = 0\\ \frac{1}{K} \sum_{m = 1}^K Y_{j(m)} & \text{ if } T_i = 1\end{cases}\]
- 最適 \(k\) を決める理論的基準は無し
- \(k\) を大きくすると、モデルの分散が小さくなる
- ただし、モデルの分散が小さい = バイアスが拡大
- Bias–variance trade-off
- \(k\) を変化させることによって結果がどのように変わるか観察
Caliper Matching
「カリパーマッチング」と訳される(訳されてない…?)
- 半径 \(h\) の中にある全てのケースの平均値を潜在的結果として使用
\[Y_i(T_i = 0) = \begin{cases}Y_i & \text{ if } T_i = 0\\ \frac{\sum_{j=1}^N I(T_j = 0, d(i, j) < h)\cdot Y_i}{\sum_{j=1}^N I(T_j = 0, d(i, j) < h)} & \text{ if } T_i = 1\end{cases}\]

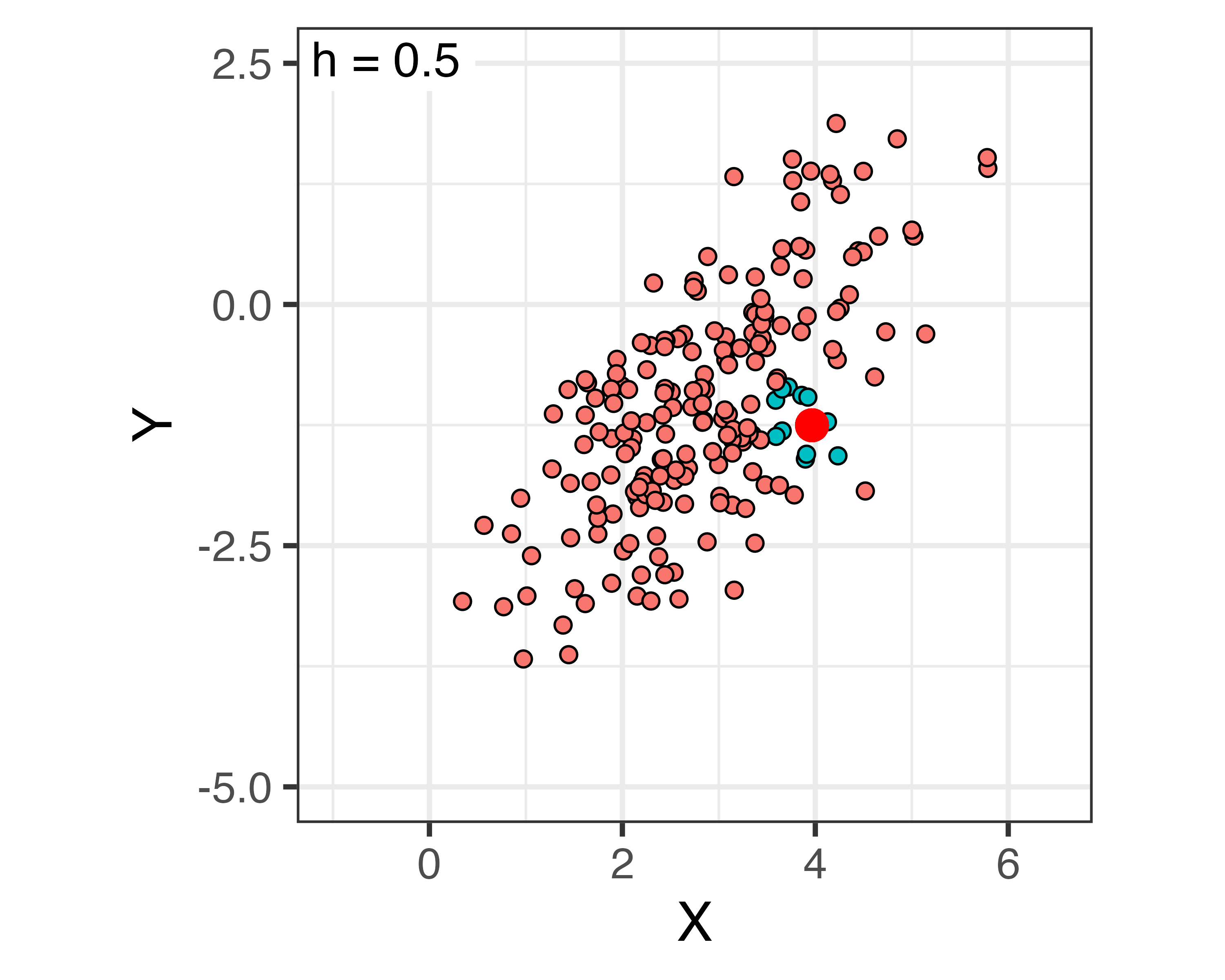
復元マッチングと非復元マッチング
- 1:1マッチングの場合に生じる問題:マッチング済みの統制群(or 処置群)をどう扱うか
- 他にも近い処置群のケースがあればマッチング \(\rightarrow\) 復元マッチング
- 他にも近い処置群のケースがあっても使わない \(\rightarrow\) 非復元マッチング
- 復元マッチングの場合、統制群の各ケースに重みが付与される。
- 加重平均 or 重み付け回帰分析が必要
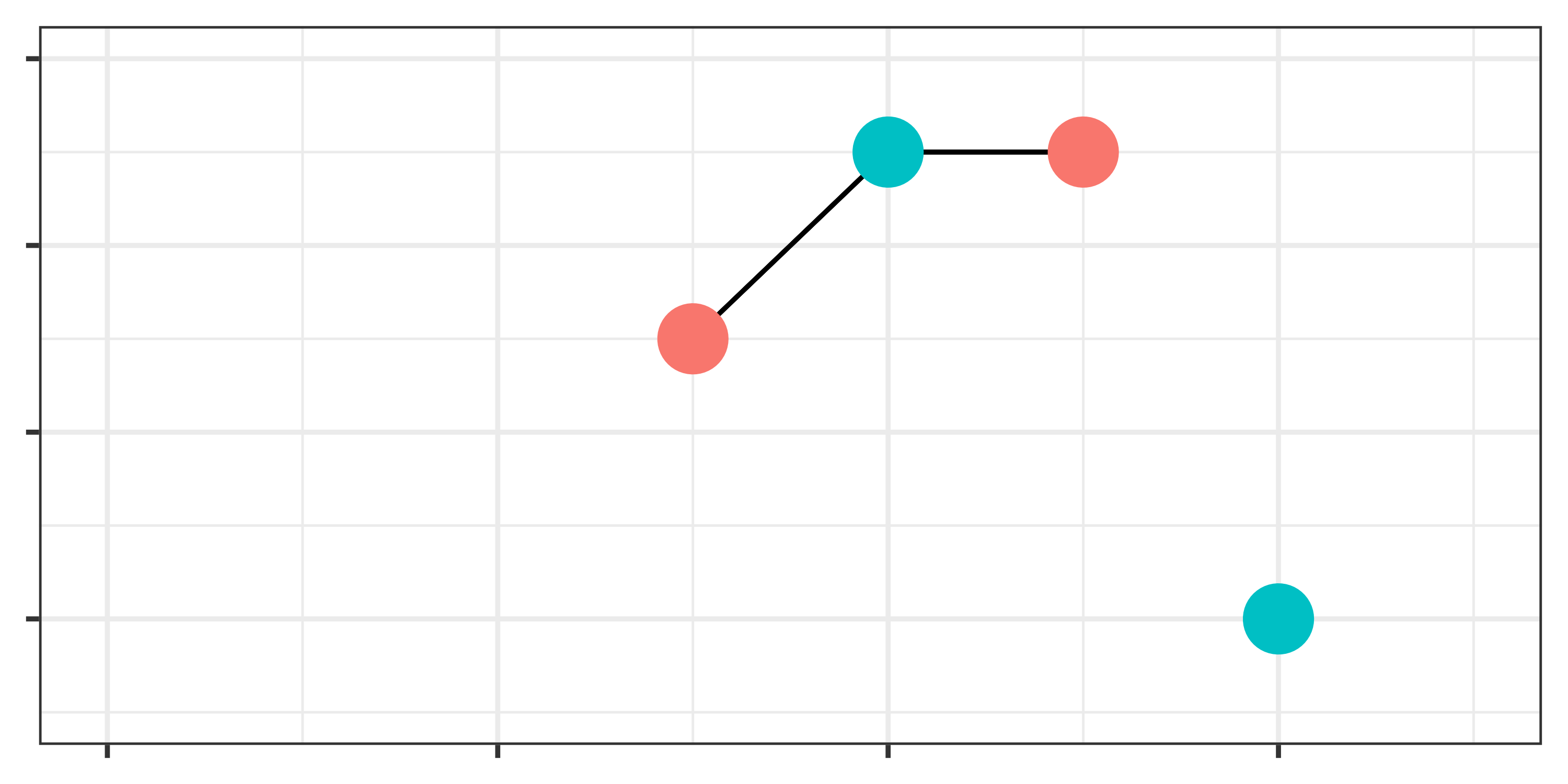
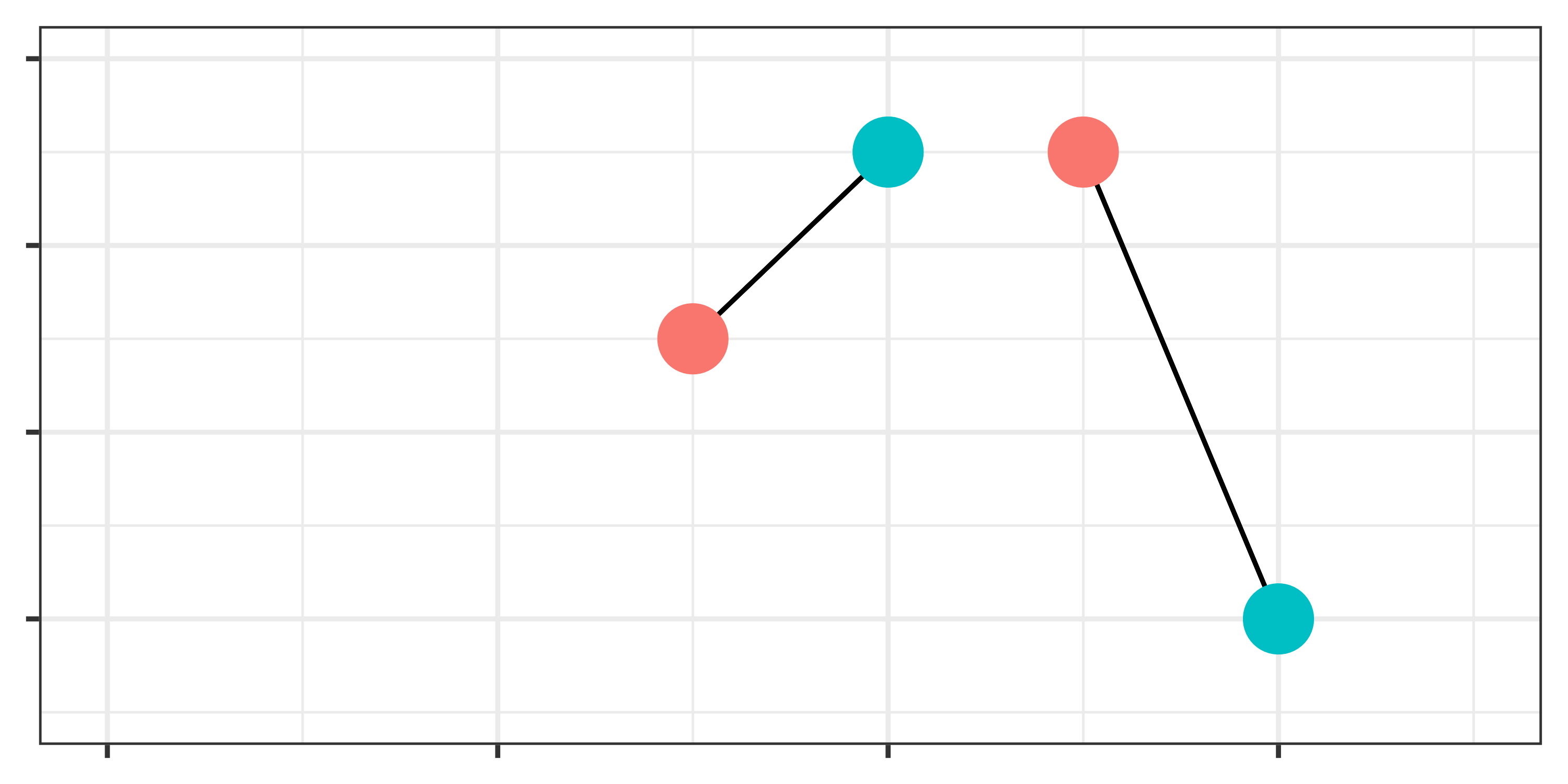
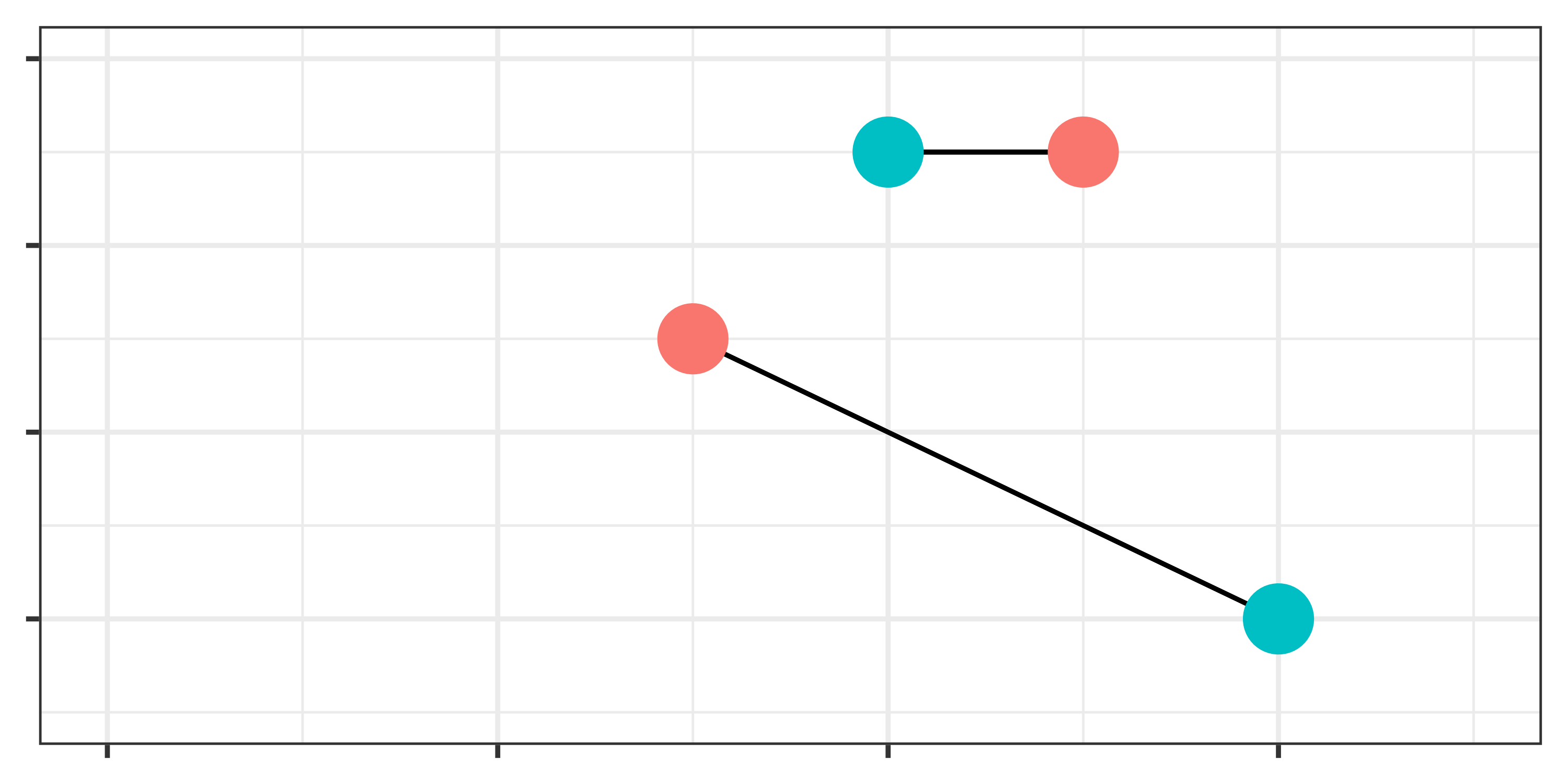
- 多くのパッケージは非復元がデフォルトとなっているが、推定ごとに結果が変化することも(図BとC)
- 復元マッチングはバランスが改善されやすいが、サンプルサイズが小さくなる。
- 正しい方法はなく、分析者の判断が必要。
- 下の例はATT推定の例(赤が処置群、青は統制群)
Coarsened Exact Matching
Coarsened Exact Matching (Iacus, King, and Porro 2011)
- 定訳はなく、「CEM」で呼ばれる(粗い正確マッチング?)
- アルゴリズムは簡単
- 共変量をいくつかの層 (strata) へ分割する。
- 各層にそれぞれ該当する処置・統制ユニットを入れる。
- 最低一つ以上の処置・統制ユニットがない層は捨てる。
- 各層の処置・統制ユニットの結果変数の差分を計算し、すべての層に対して加重平均
- 層を細かくするほどExact Matchingへ近づく
- ただし、マッチングされないケースが多くなり、分析に使えるケースが減少
- バイアス\(\downarrow\); 分散\(\uparrow\)
CEMの例
matching_data2.csvの例
- 年齢は10歳刻み、学歴は大卒以上・未満に層化
| ID | 年齢 | 教育 | 処置 | 結果 | ID | 年齢 | 教育 | 処置 | 結果 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 29 | 院 | 0 | 6 | 13 | 57 | 高 | 0 | 4 | |
| 2 | 41 | 大 | 0 | 3 | 14 | 25 | 院 | 1 | 5 | |
| 3 | 31 | 院 | 1 | 7 | 15 | 55 | 中 | 1 | 9 | |
| 4 | 39 | 院 | 0 | 5 | 16 | 48 | 院 | 0 | 2 | |
| 5 | 53 | 大 | 0 | 6 | 17 | 23 | 専 | 0 | 2 | |
| 6 | 59 | 大 | 0 | 1 | 18 | 34 | 大 | 1 | 4 | |
| 7 | 37 | 高 | 1 | 8 | 19 | 42 | 大 | 1 | 9 | |
| 8 | 44 | 中 | 0 | 4 | 20 | 23 | 高 | 0 | 4 | |
| 9 | 51 | 中 | 0 | 2 | 21 | 22 | 高 | 1 | 8 | |
| 10 | 59 | 小 | 1 | 8 | 22 | 49 | 大 | 0 | 9 | |
| 11 | 21 | 大 | 1 | 4 | 23 | 45 | 高 | 1 | 6 | |
| 12 | 24 | 中 | 1 | 6 | 24 | 33 | 大 | 0 | 8 |
CEMの例
年齢は10歳刻み、学歴は大卒以上・未満に層化
- カテゴリが少なくなり、マッチングしやすくなる
| ID | 年齢 | 教育 | 処置 | 結果 | ID | 年齢 | 教育 | 処置 | 結果 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 20代 | H | 0 | 6 | 13 | 50代 | L | 0 | 4 | |
| 2 | 40代 | H | 0 | 3 | 14 | 20代 | H | 1 | 5 | |
| 3 | 30代 | H | 1 | 7 | 15 | 50代 | L | 1 | 9 | |
| 4 | 30代 | H | 0 | 5 | 16 | 40代 | H | 0 | 2 | |
| 5 | 50代 | H | 0 | 6 | 17 | 20代 | L | 0 | 2 | |
| 6 | 50代 | H | 0 | 1 | 18 | 30代 | H | 1 | 4 | |
| 7 | 30代 | L | 1 | 8 | 19 | 40代 | H | 1 | 9 | |
| 8 | 40代 | L | 0 | 4 | 20 | 20代 | L | 0 | 4 | |
| 9 | 50代 | L | 0 | 2 | 21 | 20代 | L | 1 | 8 | |
| 10 | 50代 | L | 1 | 8 | 22 | 40代 | H | 0 | 9 | |
| 11 | 20代 | H | 1 | 4 | 23 | 40代 | L | 1 | 6 | |
| 12 | 20代 | L | 1 | 6 | 24 | 30代 | H | 0 | 8 |
CEMの例
層ごとにケースをマッチング
- ペアが組めない層が存在
- 30代 & L
- 50代 & H
| 年齢 | 教育 |
処置群
|
統制群
|
||||
|---|---|---|---|---|---|---|---|
| ID | 処置 | 結果 | ID | 処置 | 結果 | ||
| 20代 | H | 11 | 1 | 5 | 1 | 0 | 6 |
| 20代 | H | 14 | 1 | 5 | |||
| 20代 | L | 12 | 1 | 6 | 17 | 0 | 2 |
| 20代 | L | 21 | 1 | 8 | 20 | 0 | 4 |
| 30代 | H | 3 | 1 | 7 | 4 | 0 | 5 |
| 30代 | H | 18 | 1 | 4 | 24 | 0 | 8 |
| 30代 | L | 7 | 1 | 8 | |||
| 40代 | H | 19 | 1 | 9 | 2 | 0 | 3 |
| 40代 | H | 16 | 0 | 2 | |||
| 40代 | H | 22 | 0 | 9 | |||
| 40代 | L | 23 | 1 | 6 | 8 | 0 | 4 |
| 50代 | H | 5 | 0 | 6 | |||
| 50代 | H | 6 | 0 | 1 | |||
| 50代 | L | 10 | 1 | 8 | 9 | 0 | 2 |
| 50代 | L | 15 | 1 | 9 | 13 | 0 | 4 |
CEMの例
ペアが組めない層を除外(30代Lと50代H)
| 年齢 | 教育 |
処置群
|
統制群
|
||||
|---|---|---|---|---|---|---|---|
| ID | 処置 | 結果 | ID | 処置 | 結果 | ||
| 20代 | H | 11 | 1 | 5 | 1 | 0 | 6 |
| 20代 | H | 14 | 1 | 5 | |||
| 20代 | L | 12 | 1 | 6 | 17 | 0 | 2 |
| 20代 | L | 21 | 1 | 8 | 20 | 0 | 4 |
| 30代 | H | 3 | 1 | 7 | 4 | 0 | 5 |
| 30代 | H | 18 | 1 | 4 | 24 | 0 | 8 |
| 40代 | H | 19 | 1 | 9 | 2 | 0 | 3 |
| 40代 | H | 16 | 0 | 2 | |||
| 40代 | H | 22 | 0 | 9 | |||
| 40代 | L | 23 | 1 | 6 | 8 | 0 | 4 |
| 50代 | L | 10 | 1 | 8 | 9 | 0 | 2 |
| 50代 | L | 15 | 1 | 9 | 13 | 0 | 4 |
CEMの例
各ユニットの重みを計算
\[w_i = \begin{cases} 1 & \text{ if } T_i = 1, \\ \frac{m_C}{m_T} \cdot \frac{m^s_T}{m^s_C} & \text{ if } T_i = 0.\end{cases}\]
- \(m_{C,T}\): 統制・処置ケースの数
- ペアを組めなかったケースはカウントしない
- \(m^s_{C,T}\): 層 \(s\) 内の統制・処置ケースの数
| 年齢 | 教育 |
処置群
|
統制群
|
||||||
|---|---|---|---|---|---|---|---|---|---|
| ID | 処置 | 結果 | 重み | ID | 処置 | 結果 | 重み | ||
| 20代 | H | 11 | 1 | 5 | 1 | 1 | 0 | 6 | 2.2 |
| 20代 | H | 14 | 1 | 5 | 1 | ||||
| 20代 | L | 12 | 1 | 6 | 1 | 17 | 0 | 2 | 1.1 |
| 20代 | L | 21 | 1 | 8 | 1 | 20 | 0 | 4 | 1.1 |
| 30代 | H | 3 | 1 | 7 | 1 | 4 | 0 | 5 | 1.1 |
| 30代 | H | 18 | 1 | 4 | 1 | 24 | 0 | 8 | 1.1 |
| 40代 | H | 19 | 1 | 9 | 1 | 2 | 0 | 3 | 0.367 |
| 40代 | H | 16 | 0 | 2 | 0.367 | ||||
| 40代 | H | 22 | 0 | 9 | 0.367 | ||||
| 40代 | L | 23 | 1 | 6 | 1 | 8 | 0 | 4 | 1.1 |
| 50代 | L | 10 | 1 | 8 | 1 | 9 | 0 | 2 | 1.1 |
| 50代 | L | 15 | 1 | 9 | 1 | 13 | 0 | 4 | 1.1 |
CEMの例
重み付け回帰分析
- \(W = \{2.200, 0.367, 1.000, 1.100, 0.000, 0.000, ..., 1.100\}^{\top}\)
- マッチングされないケースの重みは0にする(= 分析から除外される)
- \(\beta = (X^{\prime}WX)^{-1}X^{\prime}WY\)
- Rの場合、
lm(formula, data, weight = ...)で推定可能- {cem} or {MatchIt}パッケージならもっと簡単
- \(\widehat{\text{Outcome}} = 4.567 + 2.033 \cdot \text{Treat}\)
- 処置群における因果効果(ATT)= 2.033
- ATCの場合、重み付けが逆(統制群の重みを1とする)
傾向スコア
傾向スコアとは
Propensity Score
- 簡単にいうと「あるユニット\(i\)が処置を受ける確率」
- 主に\(e\)と表記する。
- \(e_i = Pr(T_i = 1 | X_i)\)
傾向スコアの計算
処置変数(\(T_i\))を応答変数とし、共変量(\(X_i\))を説明変数とする。
- 一般的に、ロジットやプロビット回帰分析で推定する。
- 他にも色々ある
- Support Vector Machine, Decision Tree, Neural Network, …
- 色んな手法で算出した傾向スコアを重み付けして合成することも可能
- Ensemble Method(Samii, Paler, and Zukerman 2016)
- 他にも色々ある
- 推定された予測確率 \(\rightarrow\) 傾向スコア
- Rでは
オブジェクト名$fitted.valueで抽出可 - 傾向スコアは多くの共変量を一つの変数に集約したもの
- \(\rightarrow\) 傾向スコアを統制した回帰分析で因果効果を推定
- \(\rightarrow\) 傾向スコアを用いて最近傍マッチング
- Rでは
傾向スコア・マッチングの手順
割り当てメカニズムを仮定
\[Pr(\text{処置}) \propto \beta_0 + \beta_1 \cdot \text{年齢} + \beta_2 \cdot \text{教育}\]
- 参考)教育水準
- 1:小
- 2:中
- 3:高
- 4:専
- 5:大
- 6:院
| ID | 年齢 | 教育 | 処置 | 結果 | ID | 年齢 | 教育 | 処置 | 結果 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 29 | 6 | 0 | 6 | 13 | 57 | 3 | 0 | 4 | |
| 2 | 41 | 5 | 0 | 3 | 14 | 25 | 6 | 1 | 5 | |
| 3 | 31 | 6 | 1 | 7 | 15 | 55 | 2 | 1 | 9 | |
| 4 | 39 | 6 | 0 | 5 | 16 | 48 | 6 | 0 | 2 | |
| 5 | 53 | 5 | 0 | 6 | 17 | 23 | 4 | 0 | 2 | |
| 6 | 59 | 5 | 0 | 1 | 18 | 34 | 5 | 1 | 4 | |
| 7 | 37 | 3 | 1 | 8 | 19 | 42 | 5 | 1 | 9 | |
| 8 | 44 | 2 | 0 | 4 | 20 | 23 | 3 | 0 | 4 | |
| 9 | 51 | 2 | 0 | 2 | 21 | 22 | 3 | 1 | 8 | |
| 10 | 59 | 1 | 1 | 8 | 22 | 49 | 5 | 0 | 9 | |
| 11 | 21 | 5 | 1 | 4 | 23 | 45 | 3 | 1 | 6 | |
| 12 | 24 | 2 | 1 | 6 | 24 | 33 | 5 | 0 | 8 |
傾向スコアの算出
傾向スコアの算出
| (1) | |
|---|---|
| (Intercept) | 3.839 (2.364) |
| Age | -0.059 (0.039) |
| Edu | -0.420 (0.304) |
| Num.Obs. | 24 |
| AIC | 35.5 |
| F | 1.486 |
予測確率の抽出
1 2 3 4 5 6 7 8
0.4057364 0.3393856 0.3777795 0.2751913 0.2025844 0.1515735 0.6006657 0.6028218
9 10 11 12 13 14 15 16
0.5016153 0.4891956 0.6242461 0.8307399 0.3174741 0.4633432 0.4431796 0.1829360
17 18 19 20 21 22 23 24
0.6921133 0.4365297 0.3263554 0.7737818 0.7838885 0.2431492 0.4847003 0.4510136 傾向スコアの算出
傾向スコアの抽出
| ID | 年齢 | 教育 | 処置 | 結果 | PS | ID | 年齢 | 教育 | 処置 | 結果 | PS | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 29 | 6 | 0 | 6 | 0.406 | 13 | 57 | 3 | 0 | 4 | 0.317 | |
| 2 | 41 | 5 | 0 | 3 | 0.339 | 14 | 25 | 6 | 1 | 5 | 0.463 | |
| 3 | 31 | 6 | 1 | 7 | 0.378 | 15 | 55 | 2 | 1 | 9 | 0.443 | |
| 4 | 39 | 6 | 0 | 5 | 0.275 | 16 | 48 | 6 | 0 | 2 | 0.183 | |
| 5 | 53 | 5 | 0 | 6 | 0.203 | 17 | 23 | 4 | 0 | 2 | 0.692 | |
| 6 | 59 | 5 | 0 | 1 | 0.152 | 18 | 34 | 5 | 1 | 4 | 0.437 | |
| 7 | 37 | 3 | 1 | 8 | 0.601 | 19 | 42 | 5 | 1 | 9 | 0.326 | |
| 8 | 44 | 2 | 0 | 4 | 0.603 | 20 | 23 | 3 | 0 | 4 | 0.774 | |
| 9 | 51 | 2 | 0 | 2 | 0.502 | 21 | 22 | 3 | 1 | 8 | 0.784 | |
| 10 | 59 | 1 | 1 | 8 | 0.489 | 22 | 49 | 5 | 0 | 9 | 0.243 | |
| 11 | 21 | 5 | 1 | 4 | 0.624 | 23 | 45 | 3 | 1 | 6 | 0.485 | |
| 12 | 24 | 2 | 1 | 6 | 0.831 | 24 | 33 | 5 | 0 | 8 | 0.451 |
傾向スコアの算出
ATT: 傾向スコアが最も近い統制群を割り当てる
- 復元マッチングの例
処置群
|
統制群
|
差分 | |||||
|---|---|---|---|---|---|---|---|
| ID | 結果 | PS | ID | 結果 | PS | ||
| 3 | 7 | 0.378 | 1 | 6 | 0.406 | 1 | |
| 7 | 8 | 0.601 | 8 | 4 | 0.603 | 4 | |
| 10 | 8 | 0.489 | 9 | 2 | 0.502 | 6 | |
| 11 | 4 | 0.624 | 8 | 4 | 0.603 | 0 | |
| 12 | 6 | 0.831 | 20 | 4 | 0.774 | 2 | |
| 14 | 5 | 0.463 | 24 | 8 | 0.451 | -3 | |
| 15 | 9 | 0.443 | 24 | 8 | 0.451 | 1 | |
| 18 | 4 | 0.437 | 24 | 8 | 0.451 | -4 | |
| 19 | 9 | 0.326 | 13 | 4 | 0.317 | 5 | |
| 21 | 8 | 0.784 | 20 | 4 | 0.774 | 4 | |
| 23 | 6 | 0.485 | 9 | 2 | 0.502 | 4 | |
| 差分の平均値 (ATT): 1.818 | |||||||
傾向スコアの算出
ATC: 傾向スコアが最も近い処置群を割り当てる
処置群
|
統制群
|
差分 | |||||
|---|---|---|---|---|---|---|---|
| ID | 結果 | PS | ID | 結果 | PS | ||
| 3 | 7 | 0.378 | 1 | 6 | 0.406 | 1 | |
| 19 | 9 | 0.326 | 2 | 3 | 0.339 | 6 | |
| 19 | 9 | 0.326 | 4 | 5 | 0.275 | 4 | |
| 19 | 9 | 0.326 | 5 | 6 | 0.203 | 3 | |
| 19 | 9 | 0.326 | 6 | 1 | 0.152 | 8 | |
| 7 | 8 | 0.601 | 8 | 4 | 0.603 | 4 | |
| 10 | 8 | 0.489 | 9 | 2 | 0.502 | 6 | |
| 19 | 9 | 0.326 | 13 | 4 | 0.317 | 5 | |
| 19 | 9 | 0.326 | 16 | 2 | 0.183 | 7 | |
| 11 | 4 | 0.624 | 17 | 2 | 0.692 | 2 | |
| 21 | 8 | 0.784 | 20 | 4 | 0.774 | 4 | |
| 19 | 9 | 0.326 | 22 | 9 | 0.243 | 0 | |
| 15 | 9 | 0.443 | 24 | 8 | 0.451 | 1 | |
| 差分の平均値 (ATC): 3.923 | |||||||
傾向スコアの算出
ATE: ATTとATCの加重平均
\[\begin{align}\text{ATE} & = \frac{N_\text{Treat}}{N_\text{All}}\text{ATT} + \frac{N_\text{Control}}{N_\text{All}}\text{ATC} \\ & = \frac{11}{24} 1.818 + \frac{13}{24} 3.923 = 2.958\end{align}\]
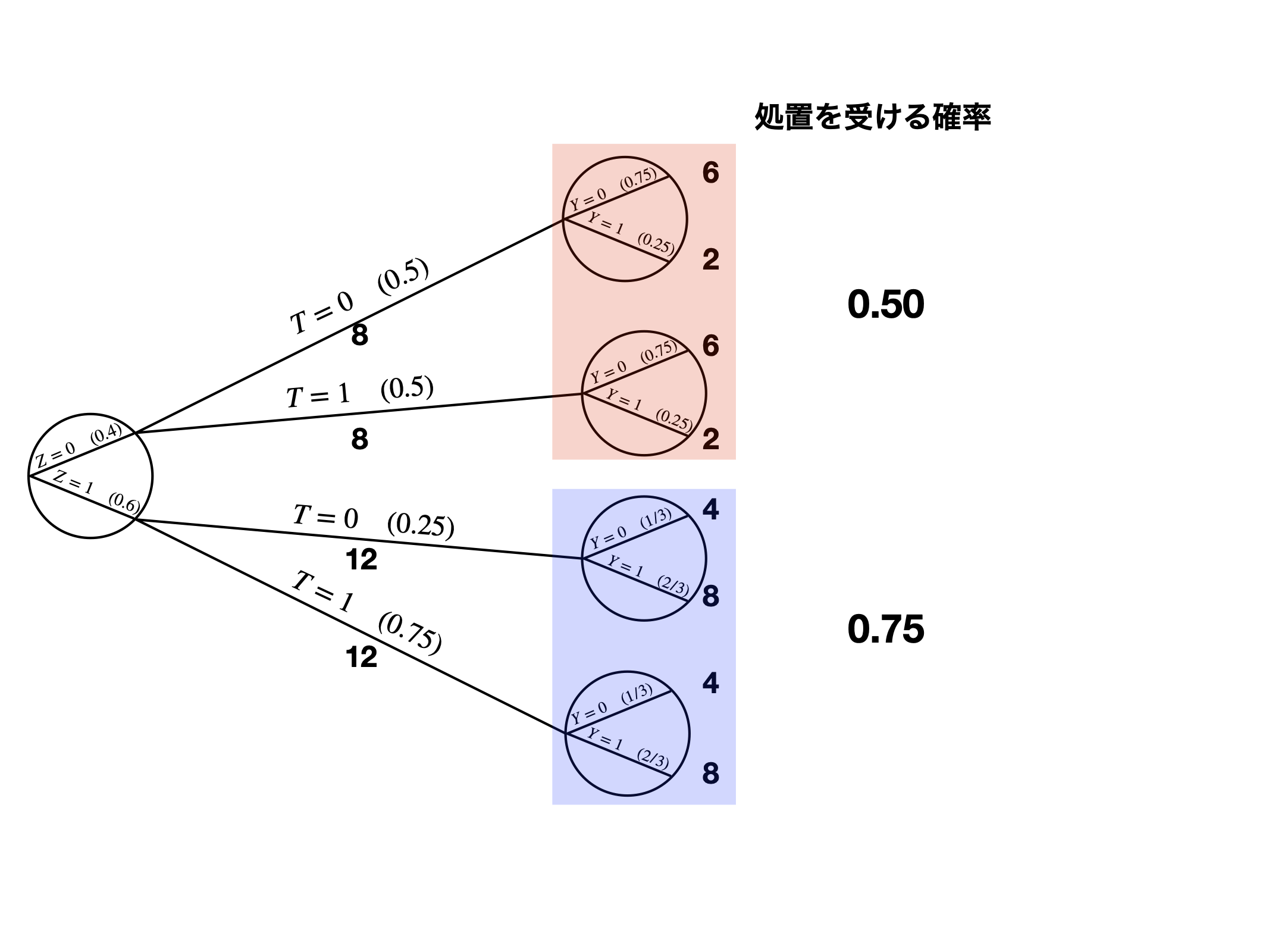
処置を受ける確率の計算
処置を受ける確率 = 傾向スコア
- 一般的にはロジスティック/プロビット回帰分析が使われる
- ただし、確率が予測できるなら他の手法でも良い
- Covariate Balancing Propensity Score
- Entropy Balancing
- Neural Network
- Support Vector Machine(SVM)
- Random Forest(RF)など
- 複数の手法を組み合わせる(= ensemble)することも可能
- \(\rightarrow\) Super Learner Algorithm
傾向スコアのもう一つの使い方
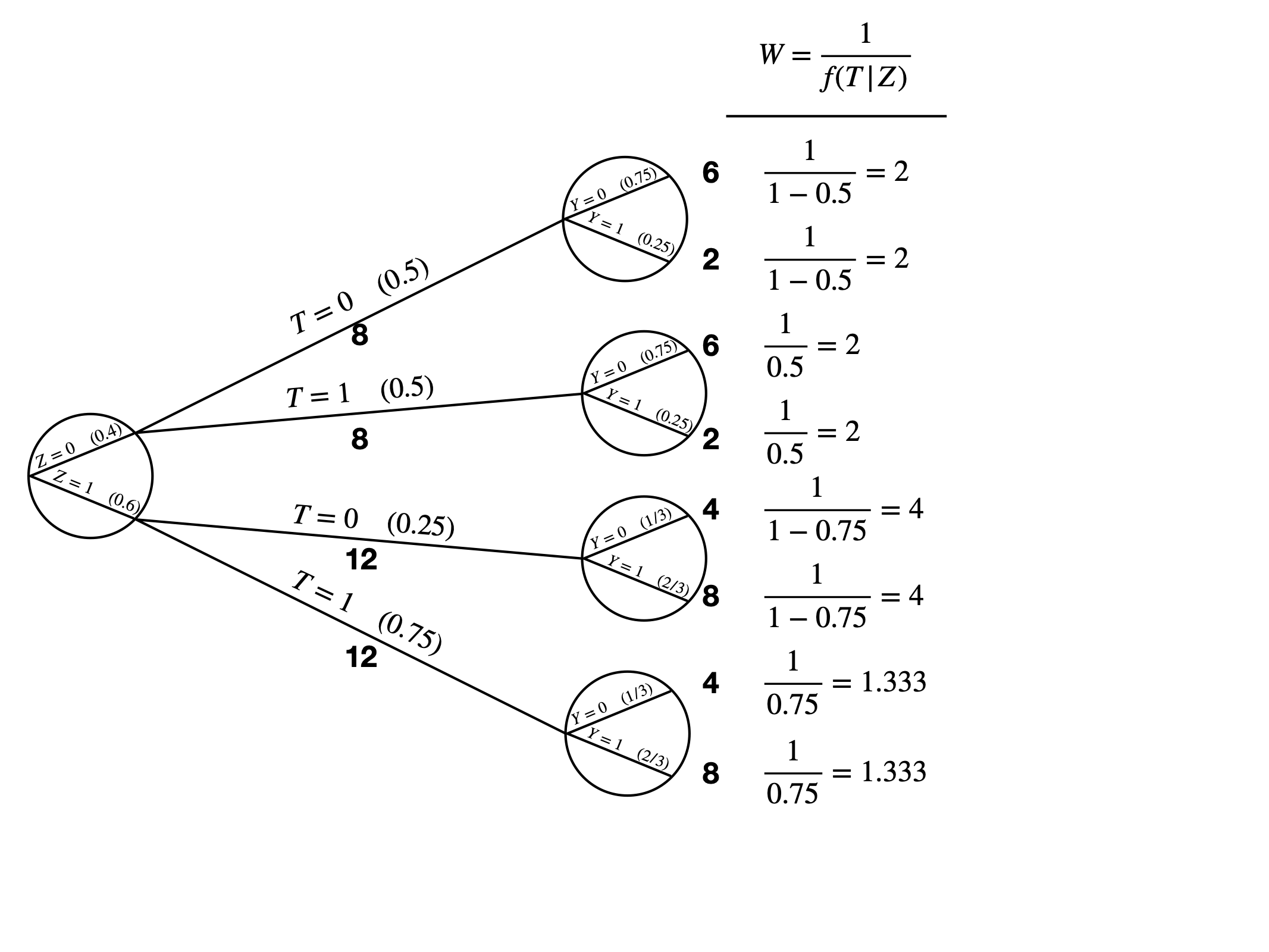
IPW: Inverse Probability Weighting (Rubin 1985)
- 「逆確率重み付け」と訳される
- 実際に処置を受けた( \(T_i = 1\) )にもかかわらず、処置を受ける傾向が 小さい場合は分析において大きい重み
- 傾向スコアを重み変数として用いる。
- \(e_i\) が1または0に近い場合、一部のケースに非常に大きい重みを付け ることになるため、注意が必要
\[w_i = \begin{cases}\frac{1}{e_i} & \text{ if } T_i = 1, \\ \frac{1}{1 - e_i} & \text{ if } T_i = 0.\end{cases}\]
- \(e_i\) : \(i\) の傾向スコア
- \(T_i\) : \(i\) の処置有無 ( \(T_i \in \{0, 1\}\) )
傾向スコアのもう一つの使い方
IPW: Inverse Probability Weighting (Rubin 1985)
- 「逆確率重み付け」と訳される
- 実際に処置を受けた( \(T_i = 1\) )にもかかわらず、処置を受ける傾向が 小さい場合は分析において大きい重み
- 傾向スコアを重み変数として用いる。
- \(e_i\) が1または0に近い場合、一部のケースに非常に大きい重みを付け ることになるため、注意が必要
\[w_i = T_i \frac{1}{e_i} + (1 - T_i) \frac{1}{1 - e_i}.\]
- \(e_i\) : \(i\) の傾向スコア
- \(T_i\) : \(i\) の処置有無 ( \(T_i \in \{0, 1\}\) )
IPW の考え方
| ID (i) | Zi | Ti | Y0, i | Y1, i |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 0 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 0 | 0 |
| 8 | 0 | 1 | 0 | 1 |
| 9 | 1 | 0 | 1 | 1 |
| 10 | 1 | 0 | 1 | 0 |
| 11 | 1 | 0 | 0 | 1 |
| 12 | 1 | 1 | 1 | 1 |
| 13 | 1 | 1 | 1 | 1 |
| 14 | 1 | 1 | 0 | 1 |
| 15 | 1 | 1 | 0 | 1 |
| 16 | 1 | 1 | 0 | 1 |
| 17 | 1 | 1 | 1 | 1 |
| 18 | 1 | 1 | 1 | 0 |
| 19 | 1 | 1 | 1 | 0 |
| 20 | 1 | 1 | 1 | 0 |
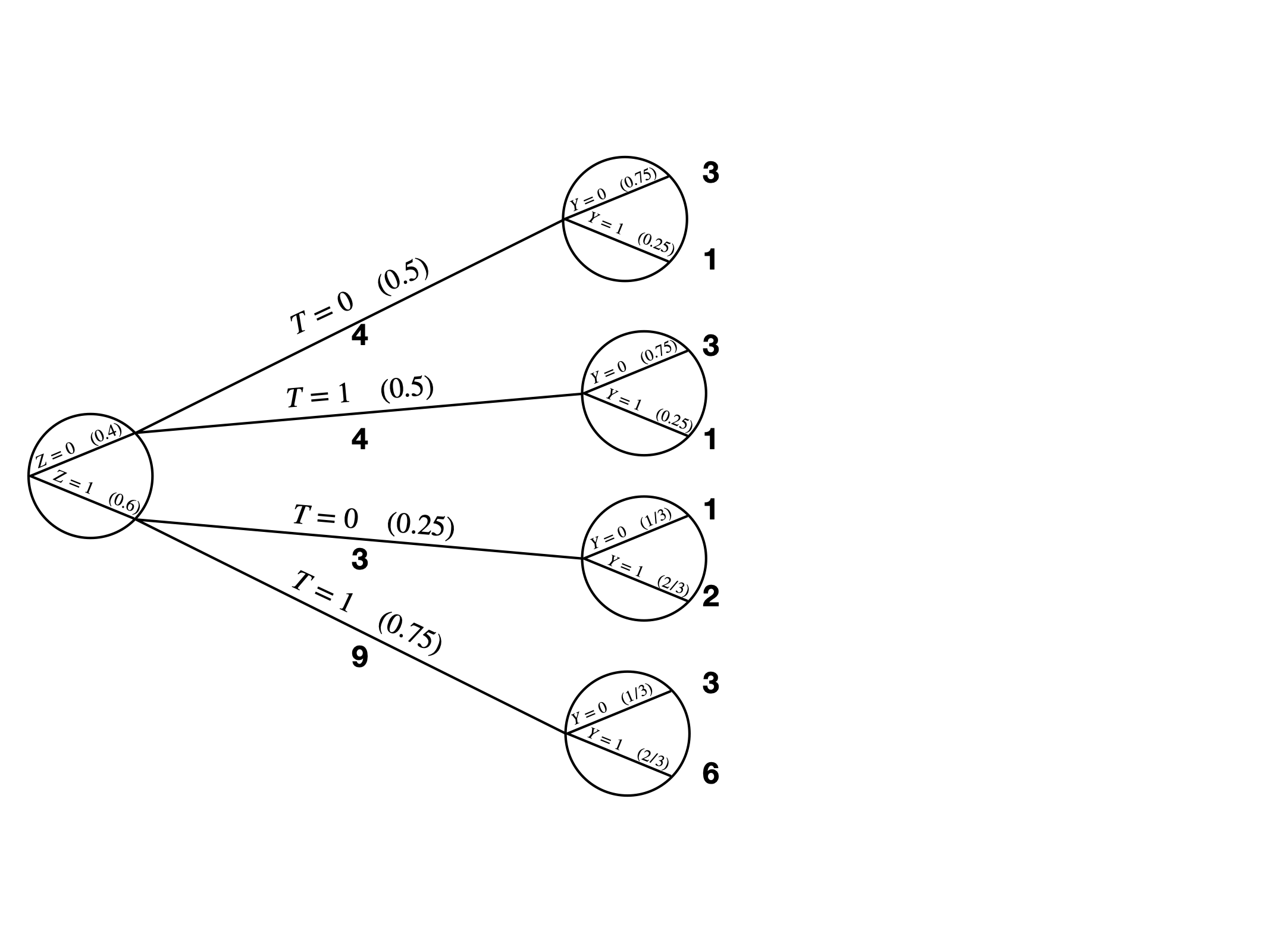
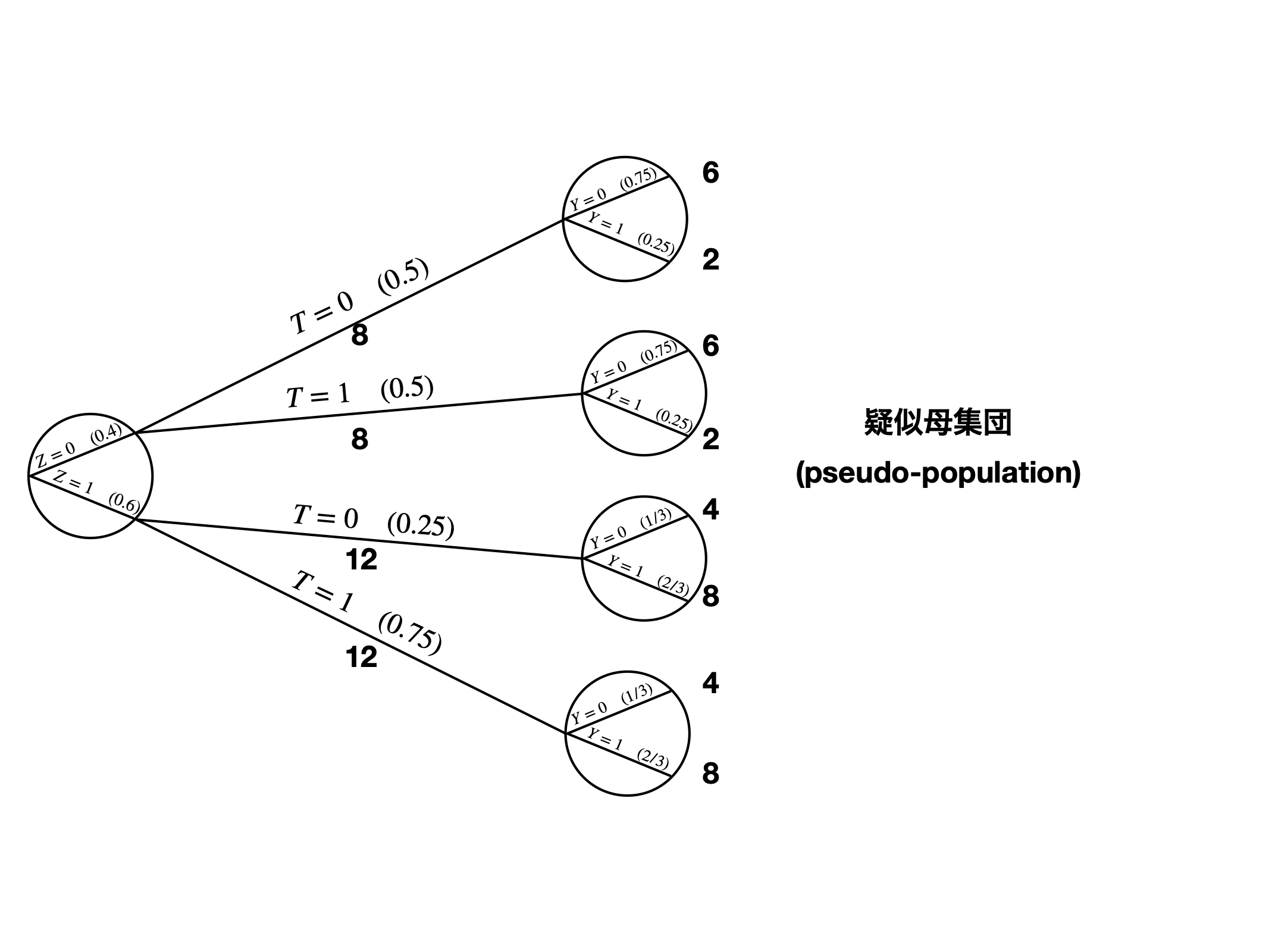
条件付き独立の例のデータ(matching_data3.csv)
- \(Pr(Z = 0) = 0.4\) 、 \(Pr(Z = 1) = 0.6\)
- \(Z = 0\) の場合
- \(Pr(T = 0) = 0.5\) 、 \(Pr(T = 1) = 0.5\)
- \(Z = 1\) の場合
- \(Pr(T = 0) = 0.25\) 、 \(Pr(T = 1) = 0.75\)
- 観察されたデータからは約0.1の処置効果が推定されるが、本当の処置効果は0
IPWの考え方
他の考え方
| ID (i) | Zi | Ti | Y0, i | Y1, i | ei | Wi |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | ? | 0.50 | 2.00 |
| 2 | 0 | 0 | 1 | ? | 0.50 | 2.00 |
| 3 | 0 | 0 | 0 | ? | 0.50 | 2.00 |
| 4 | 0 | 0 | 0 | ? | 0.50 | 2.00 |
| 5 | 0 | 1 | ? | 0 | 0.50 | |
| 6 | 0 | 1 | ? | 0 | 0.50 | |
| 7 | 0 | 1 | ? | 0 | 0.50 | |
| 8 | 0 | 1 | ? | 1 | 0.50 | |
| 9 | 1 | 0 | 1 | ? | 0.75 | 4.00 |
| 10 | 1 | 0 | 1 | ? | 0.75 | 4.00 |
| 11 | 1 | 0 | 0 | ? | 0.75 | 4.00 |
| 12 | 1 | 1 | ? | 1 | 0.75 | |
| 13 | 1 | 1 | ? | 1 | 0.75 | |
| 14 | 1 | 1 | ? | 1 | 0.75 | |
| 15 | 1 | 1 | ? | 1 | 0.75 | |
| 16 | 1 | 1 | ? | 1 | 0.75 | |
| 17 | 1 | 1 | ? | 1 | 0.75 | |
| 18 | 1 | 1 | ? | 0 | 0.75 | |
| 19 | 1 | 1 | ? | 0 | 0.75 | |
| 20 | 1 | 1 | ? | 0 | 0.75 |
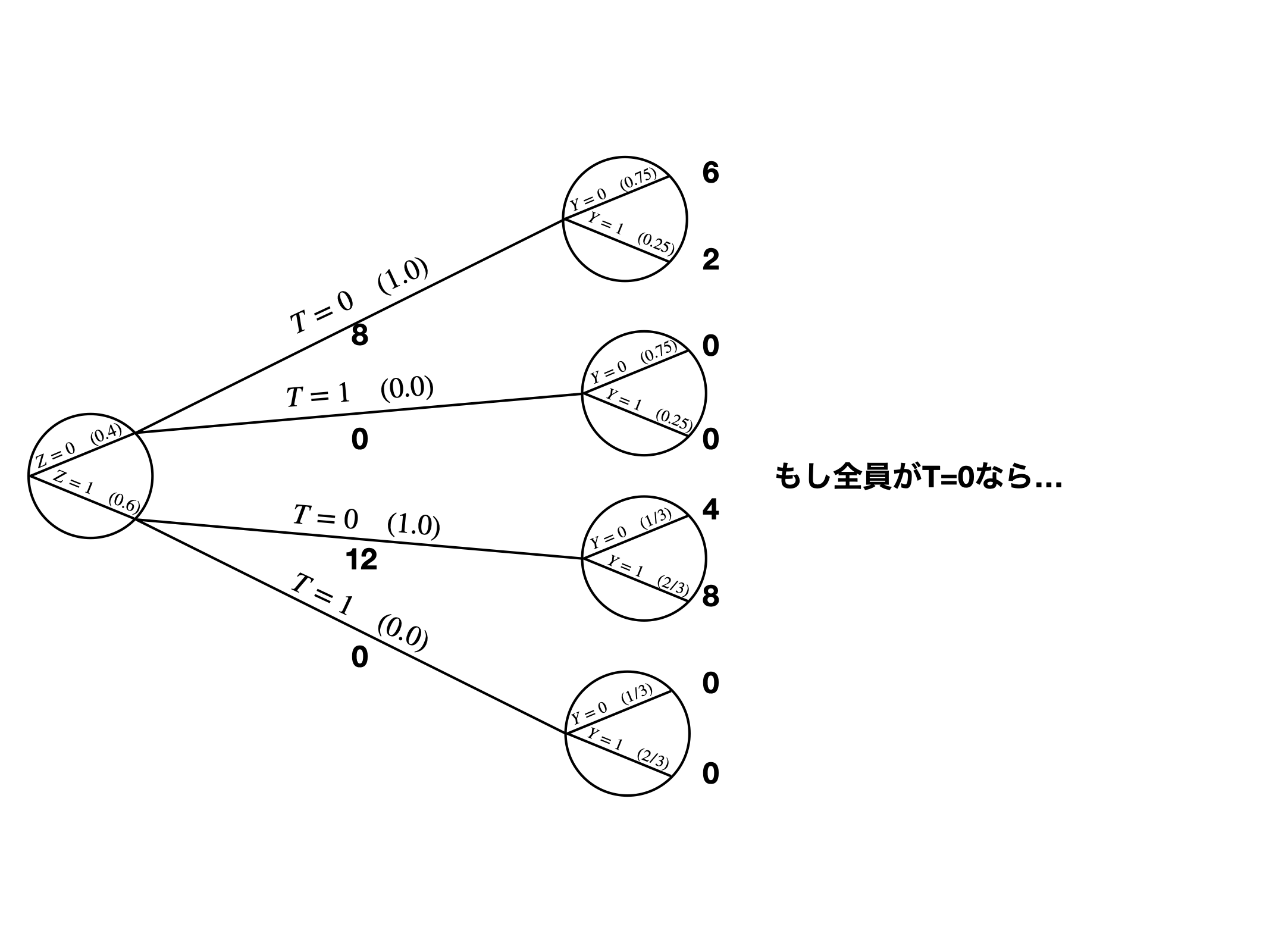
もし、全ケースが統制群なら?
- \(Z = 0\) の統制群は4ケース(ID = 1, 2, 3, 4)
- \(Z = 0\) は全部で8ケース(2倍)
- \(\rightarrow\) ケース1〜4の重みを2倍に(\(W = 2\))
- \(Z = 1\) の統制群は3ケース(ID = 9, 10, 11)
- \(Z = 1\) は全部で12ケース(4倍)
- \(\rightarrow\) ケース9〜11の重みを4倍に(\(W = 4\))
他の考え方
| ID (i) | Zi | Ti | Y0, i | Y1, i | ei | Wi |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | ? | 0.50 | |
| 2 | 0 | 0 | 1 | ? | 0.50 | |
| 3 | 0 | 0 | 0 | ? | 0.50 | |
| 4 | 0 | 0 | 0 | ? | 0.50 | |
| 5 | 0 | 1 | ? | 0 | 0.50 | 2.00 |
| 6 | 0 | 1 | ? | 0 | 0.50 | 2.00 |
| 7 | 0 | 1 | ? | 0 | 0.50 | 2.00 |
| 8 | 0 | 1 | ? | 1 | 0.50 | 2.00 |
| 9 | 1 | 0 | 1 | ? | 0.75 | |
| 10 | 1 | 0 | 1 | ? | 0.75 | |
| 11 | 1 | 0 | 0 | ? | 0.75 | |
| 12 | 1 | 1 | ? | 1 | 0.75 | 1.33 |
| 13 | 1 | 1 | ? | 1 | 0.75 | 1.33 |
| 14 | 1 | 1 | ? | 1 | 0.75 | 1.33 |
| 15 | 1 | 1 | ? | 1 | 0.75 | 1.33 |
| 16 | 1 | 1 | ? | 1 | 0.75 | 1.33 |
| 17 | 1 | 1 | ? | 1 | 0.75 | 1.33 |
| 18 | 1 | 1 | ? | 0 | 0.75 | 1.33 |
| 19 | 1 | 1 | ? | 0 | 0.75 | 1.33 |
| 20 | 1 | 1 | ? | 0 | 0.75 | 1.33 |
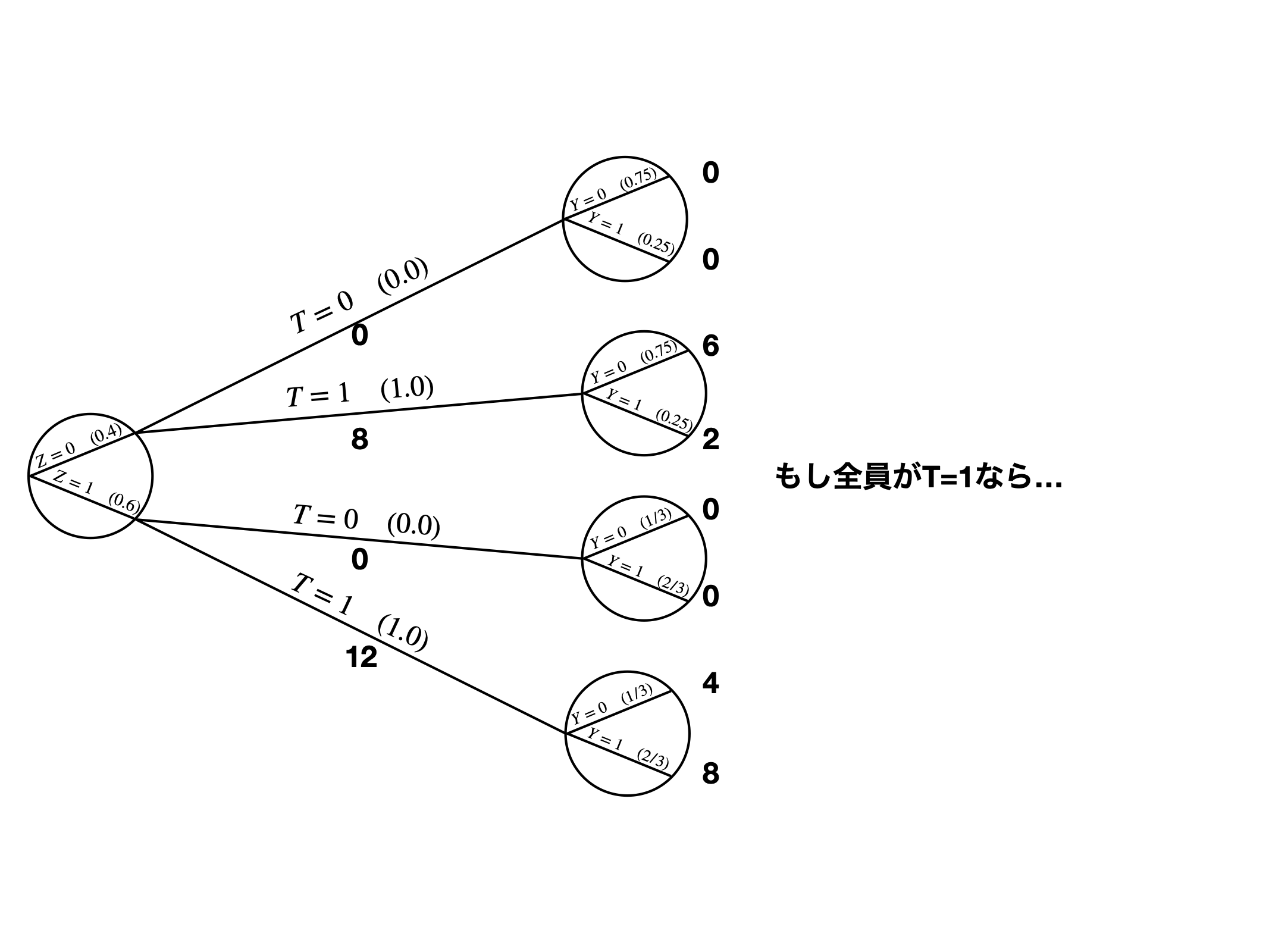
もし、全ケースが処置群なら?
- \(Z = 0\) の処置群は4ケース(ID = 5, 6, 7, 8)
- \(Z = 0\) は全部で8ケース(2倍)
- \(\rightarrow\) ケース5〜8の重みを2倍に(\(W = 2\))
- \(Z = 1\) の処置群は9ケース(ID = 12, 13, 14, … 20)
- \(Z = 1\) は全部で12ケース(1.333倍)
- \(\rightarrow\) ケース12〜20の重みを1.333倍に(\(W = 1.333\))
他の考え方
| ID (i) | Zi | Ti | Y0, i | Y1, i | ei | Wi |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | ? | 0.50 | 2.00 |
| 2 | 0 | 0 | 1 | ? | 0.50 | 2.00 |
| 3 | 0 | 0 | 0 | ? | 0.50 | 2.00 |
| 4 | 0 | 0 | 0 | ? | 0.50 | 2.00 |
| 5 | 0 | 1 | ? | 0 | 0.50 | 2.00 |
| 6 | 0 | 1 | ? | 0 | 0.50 | 2.00 |
| 7 | 0 | 1 | ? | 0 | 0.50 | 2.00 |
| 8 | 0 | 1 | ? | 1 | 0.50 | 2.00 |
| 9 | 1 | 0 | 1 | ? | 0.75 | 4.00 |
| 10 | 1 | 0 | 1 | ? | 0.75 | 4.00 |
| 11 | 1 | 0 | 0 | ? | 0.75 | 4.00 |
| 12 | 1 | 1 | ? | 1 | 0.75 | 1.33 |
| 13 | 1 | 1 | ? | 1 | 0.75 | 1.33 |
| 14 | 1 | 1 | ? | 1 | 0.75 | 1.33 |
| 15 | 1 | 1 | ? | 1 | 0.75 | 1.33 |
| 16 | 1 | 1 | ? | 1 | 0.75 | 1.33 |
| 17 | 1 | 1 | ? | 1 | 0.75 | 1.33 |
| 18 | 1 | 1 | ? | 0 | 0.75 | 1.33 |
| 19 | 1 | 1 | ? | 0 | 0.75 | 1.33 |
| 20 | 1 | 1 | ? | 0 | 0.75 | 1.33 |
- 統制群における
Wの和: 20 - 処置群における
Wの和: 20 - \(\rightarrow\) 各群における
Wの和はサンプルサイズと一致する - \(\rightarrow\) 全サンプルが統制/処置群の場合の結果変数の期待値を計算(加重平均)
他の考え方
| ID (i) | Zi | Ti | Y0, i | Y1, i | ei | Wi |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | ? | 0.50 | 2.00 |
| 2 | 0 | 0 | 1 | ? | 0.50 | 2.00 |
| 3 | 0 | 0 | 0 | ? | 0.50 | 2.00 |
| 4 | 0 | 0 | 0 | ? | 0.50 | 2.00 |
| 5 | 0 | 1 | ? | 0 | 0.50 | 2.00 |
| 6 | 0 | 1 | ? | 0 | 0.50 | 2.00 |
| 7 | 0 | 1 | ? | 0 | 0.50 | 2.00 |
| 8 | 0 | 1 | ? | 1 | 0.50 | 2.00 |
| 9 | 1 | 0 | 1 | ? | 0.75 | 4.00 |
| 10 | 1 | 0 | 1 | ? | 0.75 | 4.00 |
| 11 | 1 | 0 | 0 | ? | 0.75 | 4.00 |
| 12 | 1 | 1 | ? | 1 | 0.75 | 1.33 |
| 13 | 1 | 1 | ? | 1 | 0.75 | 1.33 |
| 14 | 1 | 1 | ? | 1 | 0.75 | 1.33 |
| 15 | 1 | 1 | ? | 1 | 0.75 | 1.33 |
| 16 | 1 | 1 | ? | 1 | 0.75 | 1.33 |
| 17 | 1 | 1 | ? | 1 | 0.75 | 1.33 |
| 18 | 1 | 1 | ? | 0 | 0.75 | 1.33 |
| 19 | 1 | 1 | ? | 0 | 0.75 | 1.33 |
| 20 | 1 | 1 | ? | 0 | 0.75 | 1.33 |
- 統制群の加重平均
- \(0 \cdot 2 + 1 \cdot 2 + 0 \cdot 2 + 0 \cdot 2 + \dots + 0 \cdot 4\)
- \(\mathbb{E}^w[Y_0] = 10\)
- 処置群の加重平均
- \(0 \cdot 2 + 0 \cdot 2 + 0 \cdot 2 + 1 \cdot 2 + \dots + 0 \cdot 1.33\)
- \(\mathbb{E}^w[Y_1] = 10\)
\[\mathbb{E}^w[Y_1] - \mathbb{E}^w[Y_0] = 0\]
共変量の選択
共変量の選択
共変量選択の基準は (星野 2009; Imbens and Rubin 2015など)
- 処置変数と結果変数、両方と連関があること
- OVBと関係
- 処置前変数と処置後変数の区別
- 処置変数に時間的に先行しているか否か
- 処置前変数 (pre-treatment variable) は必ず投入する
- 処置後変数 (post-treatment variable) は目的による
- というものの、基本的に投入しない
- 応答変数よりも時間的に後なら絶対に投入しない
共変量の選択
VanderWeele (2019) のmodified disjunctive cause criterion
- 処置変数と応答変数どちらかの原因となる変数
- 処置変数と応答変数両方の原因となる変数
- 操作変数は共変量として投入しない
- 上記の基準を満たさない場合でも、観察されていない共変量の代理変数は統制しても良い
- しかし、慎重に選択しないとバイアスが拡大
- 2.の該当する変数の代理変数が望ましい
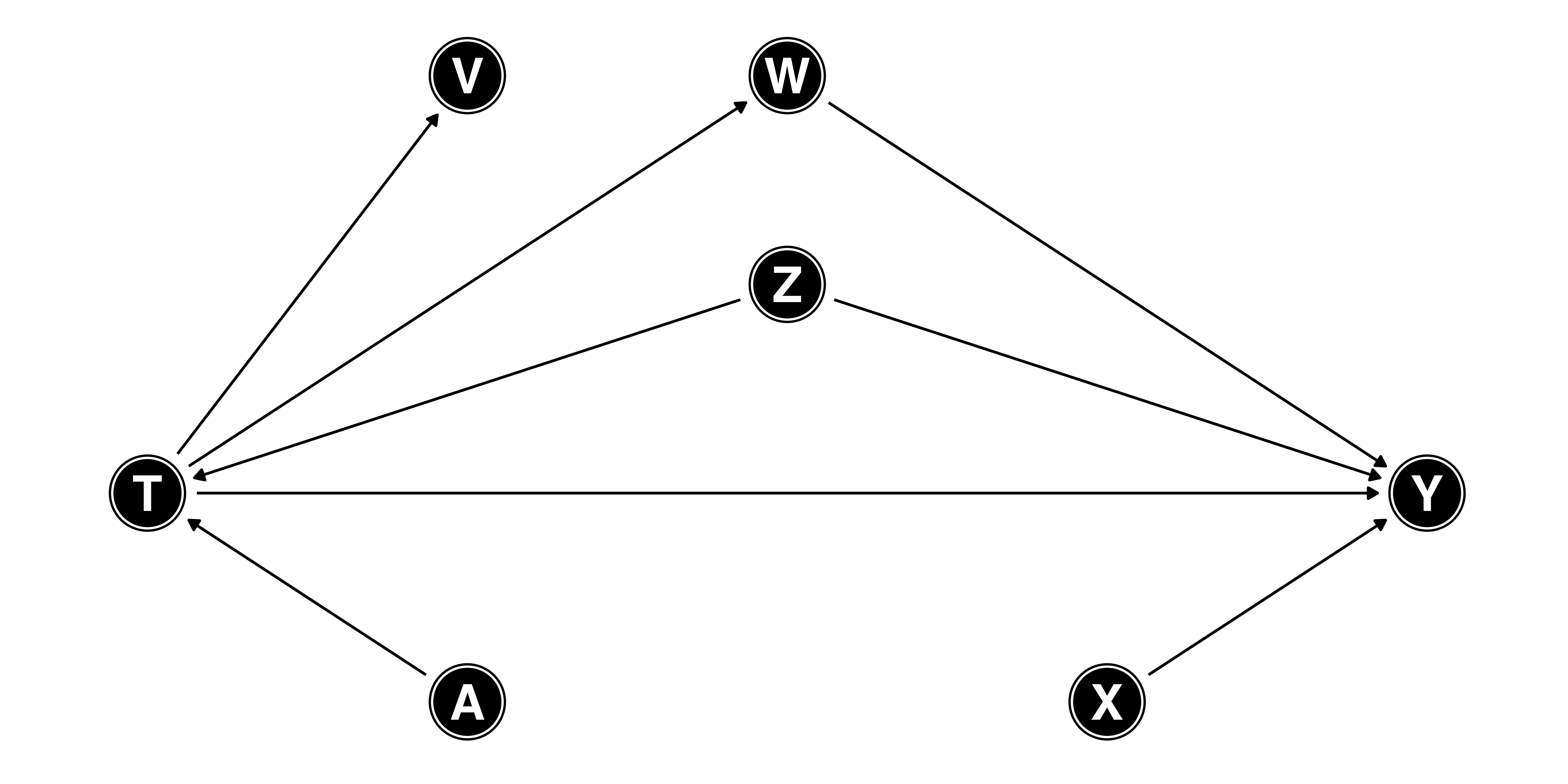
ダイアグラムを使った例
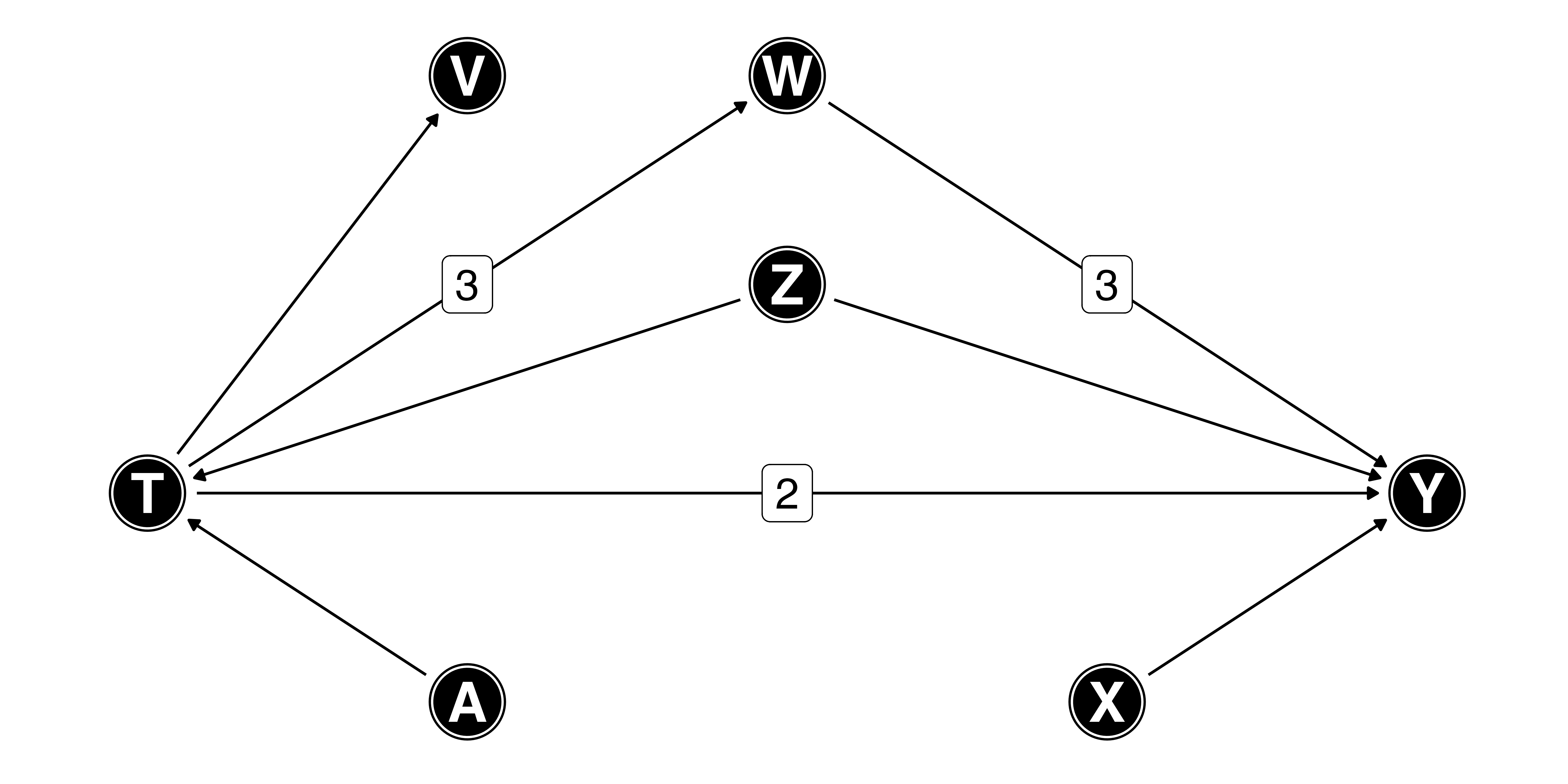
- \(T \rightarrow Y\)の効果は11
- \(Z\): \(T\)と\(Y\)の原因 \(\leftarrow\) 投入
- \(A\): 操作変数 \(\leftarrow\) 除外
- \(X\): \(Y\)の原因 \(\leftarrow\) 投入
- \(V\): \(T\)の結果 \(\leftarrow\) 除外
- \(W\)は…?
ダイアグラムを使った例
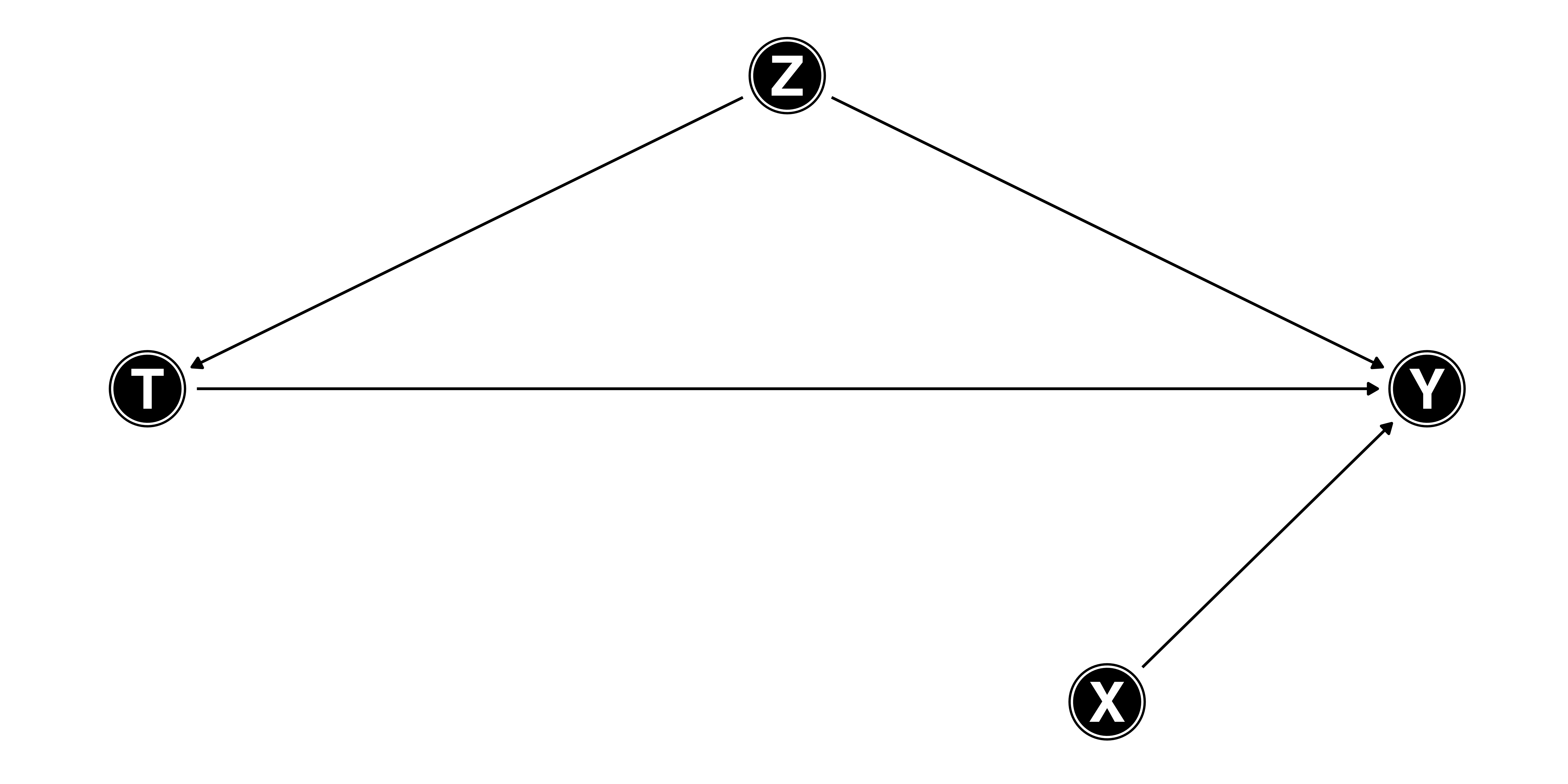
- \(T \rightarrow Y\): 直接効果
- \(T \rightarrow W \rightarrow Y\): 間接効果
- \(W\)は中間変数(mediate variable)
- 因果推論では主に全効果 (total effect) に関心があるため\(W\)は投入しない
- 全効果: 直接効果 + 間接効果
- \(T\)が変動したら\(W\)も必ず変わるため、\(T\)のみの効果はあまり意味なし
- 直接効果のみ推定する場合、\(W\)も統制
- 例) 就職市場における人種差別の例
- 結論: \(Z\)と\(X\)のみ統制
- 実は\(X\)は入れなくてもOK
ダイアグラムのツール
DAGitty — draw and analyze causal diagrams
- ウェーブページ or Rパッケージ{dagitty}
ダイアグラムのツール
{ggdag}を用いた可視化
- 詳細は『私たちのR』第22章を参照
実習
実習内容
- マッチングの実装: {MatchIt}、{WeightIt}パッケージ
- 線形回帰分析
- 最近傍マッチング(Mahalanobis Matching)
- CEM
- 傾向スコアマッチング
- IPW
- バランスチェック: {cobalt}パッケージ
- 標準化差分
- ヒストグラム
- QQ Plotなど
- マッチング手法間の比較
実習用データ: lalonde(職業訓練と所得)
lalondeは様々なパッケージがサンプルデータとして提供しているが、本講義では{cobalt}のlalondeデータセットを利用
data("lalonde", package = "cobalt")で読み込み- その前に{cobalt}パッケージを読み込む
# A tibble: 614 × 9
treat age educ race married nodegree re74 re75 re78
<int> <int> <int> <fct> <int> <int> <dbl> <dbl> <dbl>
1 1 37 11 black 1 1 0 0 9930.
2 1 22 9 hispan 0 1 0 0 3596.
3 1 30 12 black 0 0 0 0 24909.
4 1 27 11 black 0 1 0 0 7506.
5 1 33 8 black 0 1 0 0 290.
6 1 22 9 black 0 1 0 0 4056.
7 1 23 12 black 0 0 0 0 0
8 1 32 11 black 0 1 0 0 8472.
9 1 22 16 black 0 0 0 0 2164.
10 1 33 12 white 1 0 0 0 12418.
# ℹ 604 more rows| 変数名 | 説明 | |
|---|---|---|
| 1 | treat |
職業訓練の履修有無 |
| 2 | age |
年齢 |
| 3 | educ |
教育年数 |
| 4 | race |
人種 |
| 5 | married |
結婚有無 |
| 6 | nodegree |
学位有無 |
| 7 | re74 |
1974年の所得 |
| 8 | re75 |
1975年の所得 |
| 9 | re78 |
1978年の所得 |