社会科学における因果推論
3/ 内生性
1 内生性
割当メカニズム
割当メカニズム(assignment mechanism):個体\(i\)が処置を受けるメカニズム
- 以下は処置有無(D)が3つの変数(X、Z)から規定される例
- 例)GPAが高い学生が宋さんの授業を履修する
- 例)単位がやばい学生が宋さんの授業を履修する
- 例)やる気がある学生が宋さんの授業を履修するなど

内生性
内生性(endogeneity):処置変数と誤差項間に相関が存在する状態(\(\Leftrightarrow\)外生性)
- 内生性が存在する場合、処置変数は内生変数(\(\Leftrightarrow\)外生変数)と呼ばれる
- 処置変数が内生変数なら…
- 処置効果の推定量は一致(consistent)推定量でも、不偏(unbiased)推定量でもなくなる
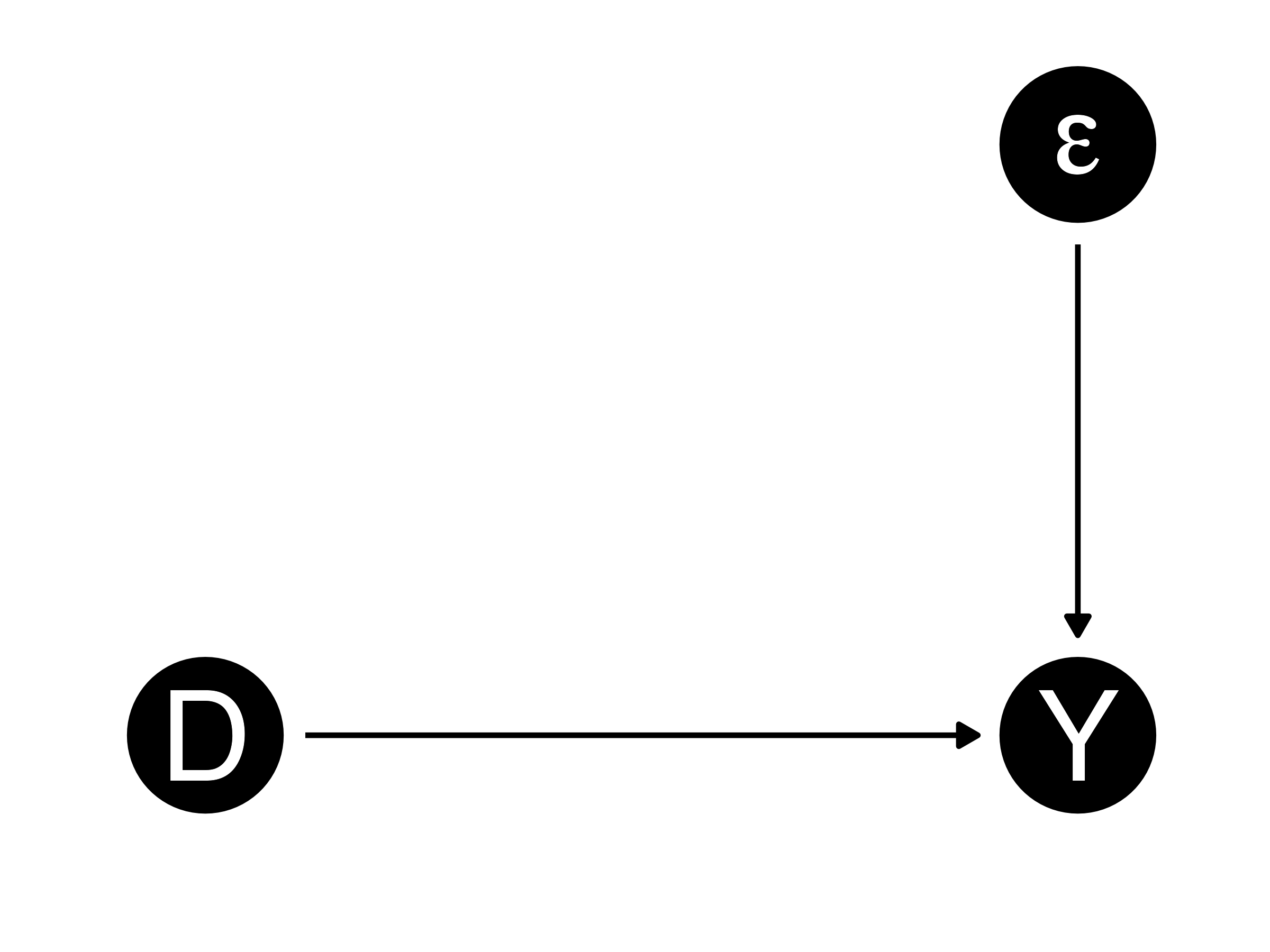
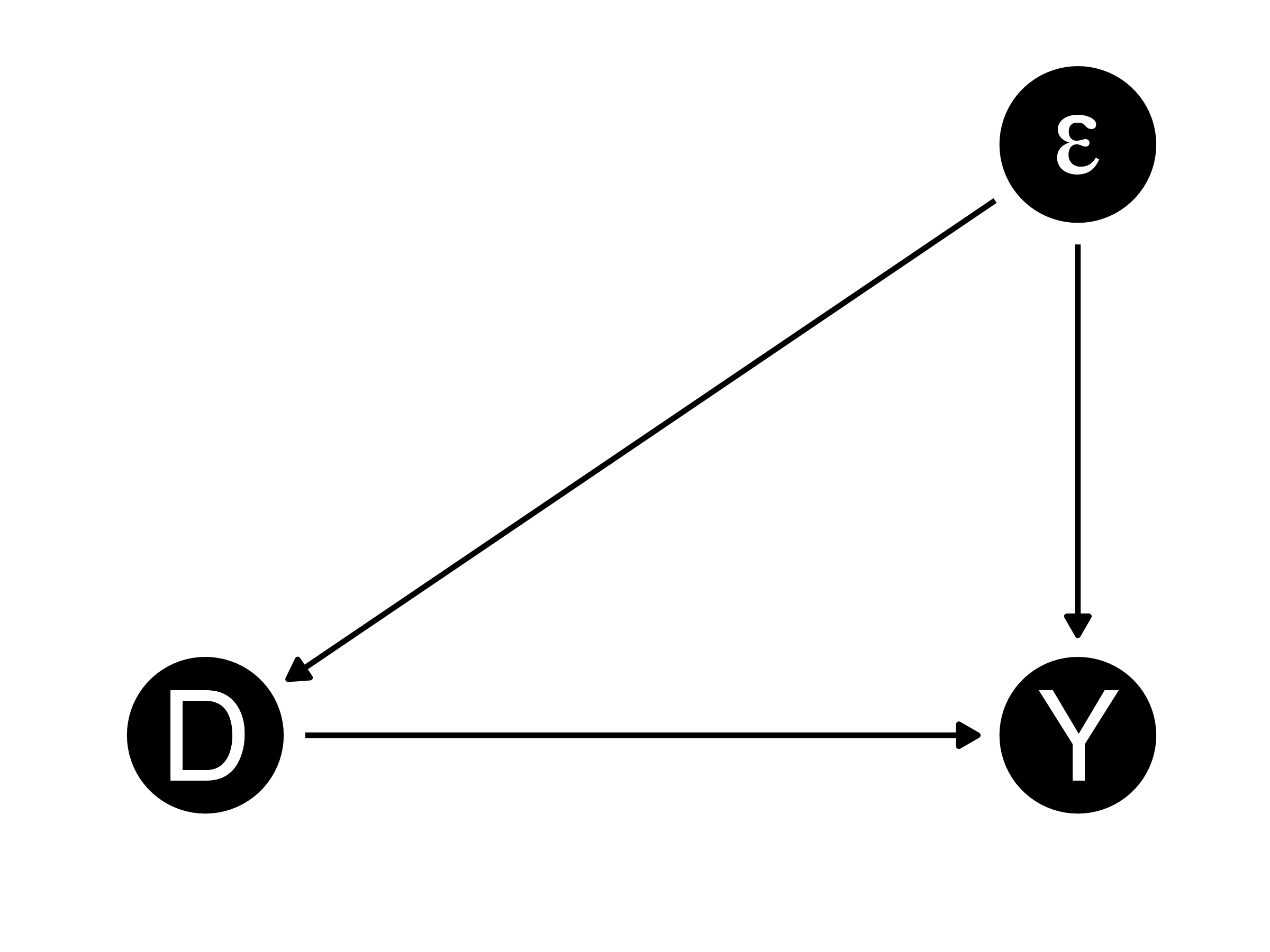
参考:誤差
例)2024年衆院選の投票率:53.8%(真の値; パラメーター)
| 調査 | \(n\) | 投票率 | 誤差 |
|---|---|---|---|
| 調査A | 100 | 0.490 | 0.048 |
| 調査B | 500 | 0.568 | 0.030 |
| 調査C | 1,000 | 0.561 | 0.023 |
| 調査D | 2,000 | 0.543 | 0.005 |
観測値 = 真の値 + 誤差
- 誤差(error):観測された値と真の値(母数; パラメーター)間のズレ
- 誤差がぴったり0になることはほぼない
- サンプルが母集団から無作為抽出されているのであれば、\(n\)が大きくなるほど誤差は0へ収斂する \(\Rightarrow\) 大数の法則1(Law of large numbers; LLM)
- ある統計量が一致推定量であれば、\(n\)を大きくすることでよりパラメーターに近い値が得られる
参考:バイアス
バイアス(偏り; bias):統計量の期待値とパラメーター間のずれ
- \(\mathbb{E}[\hat{\theta}] - \theta = 0\)の場合、\(\hat{\theta}\)は\(\theta\)の不偏推定量(unbiased estimator)
| 調査 | \(n\) | 投票率 | 誤差 |
|---|---|---|---|
| 調査A | 3,000 | 0.518 | -0.020 |
| 調査B | 1,000 | 0.514 | -0.024 |
| 調査C | 1,500 | 0.599 | 0.061 |
| 調査D | 2,000 | 0.547 | 0.009 |
| … | … | … | … |
| 調査\(\infty\) | 2,400 | 0.567 | 0.029 |
| 平均 | 0.000 |
| 調査 | \(n\) | 投票率 | 誤差 |
|---|---|---|---|
| 調査A | 3,000 | 0.635 | 0.097 |
| 調査B | 1,000 | 0.530 | -0.008 |
| 調査C | 1,500 | 0.594 | 0.056 |
| 調査D | 2,000 | 0.603 | 0.065 |
| … | … | … | … |
| 調査\(\infty\) | 2,400 | 0.585 | 0.047 |
| 平均 | 0.050 |
参考:バイアス \(\neq\) 誤差
- 誤差は観測値とパラメーター間のズレだから、一つひとつの個体が持つ
- 誤差項は特定の確率分布に従うと仮定するケースが多い(平均0の正規分布など)
- バイアスは個体でなく、特定の統計量が持つ性質
- バイアスが大きい統計量でもそれを構成する一部の個体の誤差は小さい可能性もある



内生性の発生メカニズム
- 例1)割当メカニズム上に存在する変数(XとZ)が結果変数にも影響を与えている(ここではXのみ)
- 例2)割当メカニズム上に存在する変数が観察されず、これらの変数が誤差項(\(\varepsilon\))の一部を占めている1
- Xが誤差項に含まれることによって誤差項と処置変数間の相関が発生
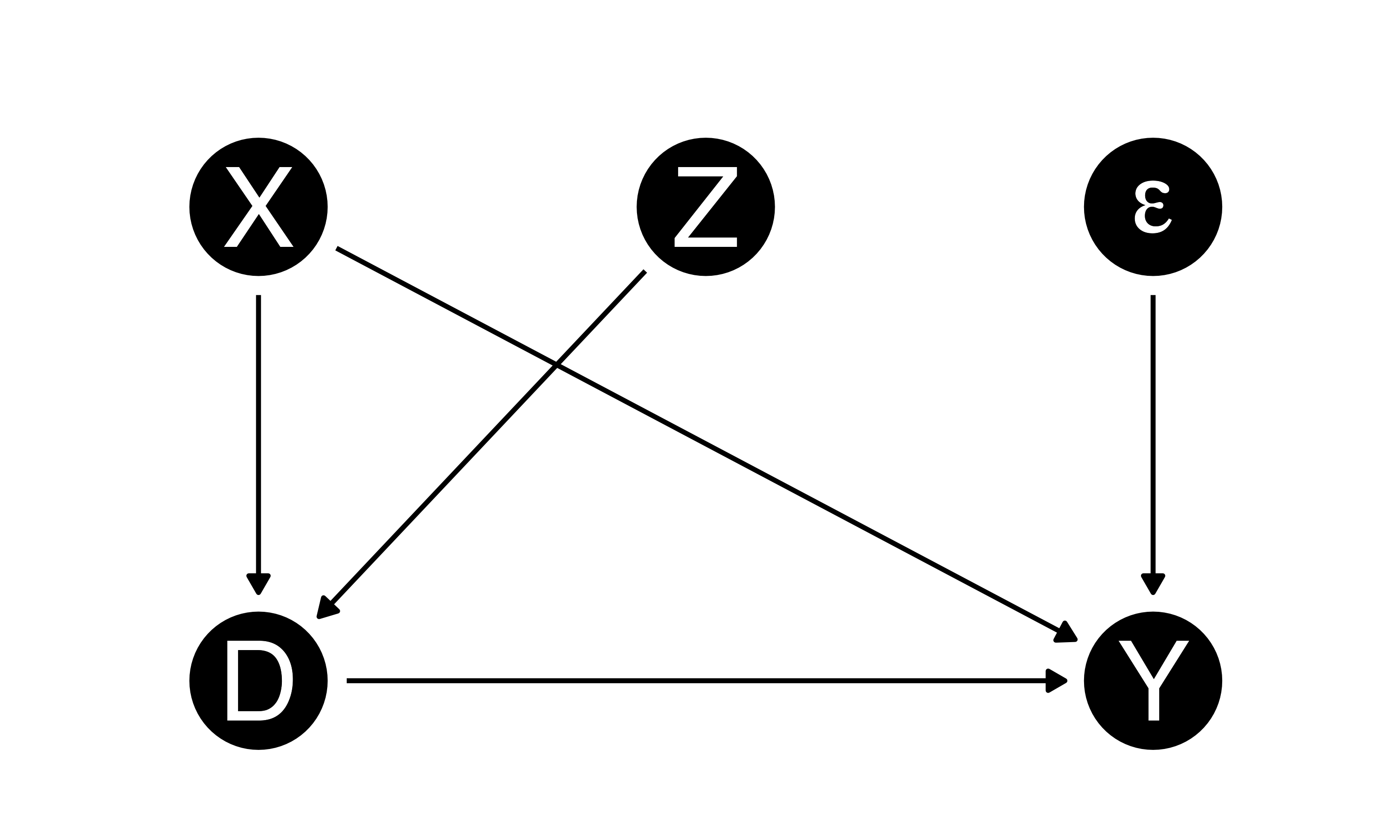
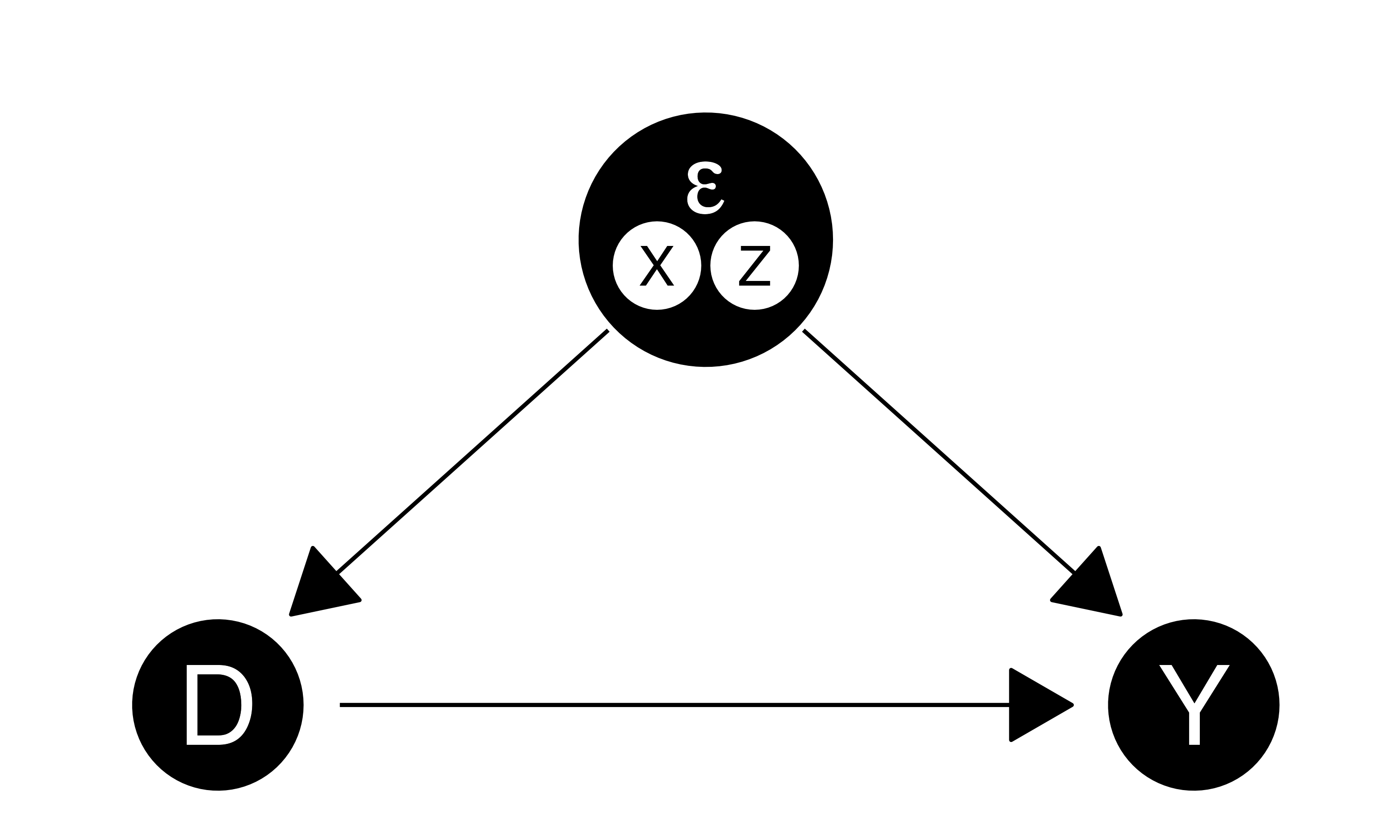
内生性の原因
処置変数と誤差項間の相関関係(内生性)は様々な理由から発生する
- セレクション・バイアス
- セルフセレクション・バイアス、サンプルセレクション・バイアスなど
- 欠落変数バイアス
- 逆の因果
- 同時性
- 測定誤差など
社会科学における因果推論上に存在する内生性はセレクション・バイアスが原因1であるケースが多い
2 セレクション・バイアス
セレクション・バイアスの定式化
- セレクション・バイアスが存在する場合、推定された因果効果(処置効果)にはセレクションによりバイアスを含む
- 推定された処置効果 = 真の処置効果 + セレクション・バイアス
- 推定対象がATTかATCかによって想定されるセレクション・バイアスが異なる
- ATT:処置群のおける処置効果(\(\mathbb{E}[Y_i(1) - Y_i(0) | D_i = 1]\))
- ATC:統制群のおける処置効果(\(\mathbb{E}[Y_i(1) - Y_i(0) | D_i = 0]\))
ATTとセレクション・バイアス
もともと優秀な人が宋さんの授業を取る(自己選択)
- \(\mathbb{E}[Y_i(0) | D_i = 1]\):処置群がもし処置を受けなかった場合の結果変数の期待値
- \(\mathbb{E}[Y_i(0) | D_i = 0]\):統制群における結果変数の期待値(観察可能)
\[ \begin{align} & \mathbb{E}[Y_i | D_i = 1] - \mathbb{E}[Y_i | D_i = 0] \\ = & \mathbb{E}[Y_i(1) | D_i = 1] - \mathbb{E}[Y_i(0) | D_i = 0] \\ = & \mathbb{E}[Y_i(1) | D_i = 1] \textcolor{red}{- \mathbb{E}[Y_i(0) | D_i = 1] + \mathbb{E}[Y_i(0) | D_i = 1]} - \mathbb{E}[Y_i(0) | D_i = 0] \\ = & \underbrace{\mathbb{E}[Y_i(1) - Y_i(0) | D_i = 1]}_{\textsf{ATT}} + \underbrace{\mathbb{E}[Y_i(0) | D_i = 1] - \mathbb{E}[Y_i(0) | D_i = 0]}_{\textsf{selection bias}} \end{align} \]
ATCとセレクション・バイアス
授業の効果が高そうな人が宋さんの授業を取る(最適化選択)
- \(\mathbb{E}[Y_i(1) | D_i = 1]\):処置群における結果変数の期待値(観察可能)
- \(\mathbb{E}[Y_i(1) | D_i = 0]\):統制群がもし処置を受けたら場合の結果変数の期待値
\[ \begin{align} & \mathbb{E}[Y_i | D_i = 1] - \mathbb{E}[Y_i | D_i = 0] \\ = & \mathbb{E}[Y_i(1) | D_i = 1] - \mathbb{E}[Y_i(0) | D_i = 0] \\ = & \mathbb{E}[Y_i(1) | D_i = 1] \textcolor{red}{- \mathbb{E}[Y_i(1) | D_i = 0] + \mathbb{E}[Y_i(1) | D_i = 0]} - \mathbb{E}[Y_i(0) | D_i = 0] \\ = & \underbrace{\mathbb{E}[Y_i(1) | D_i = 1] - \mathbb{E}[Y_i(1) | D_i = 0]}_{\textsf{selection bias}} + \underbrace{\mathbb{E}[Y_i(1) - Y_i(0) | D_i = 0]}_{\textsf{ATC}} \end{align} \]
ATT、ATCの識別条件
以下の2つの条件がすべて満たされる場合、ATEが推定可能
- ATTの識別条件
- \(\mathbb{E}[Y_i(0) | D_i = 1] = \mathbb{E}[Y_i(0) | D_i = 0]\)
- この場合、ATT = \(\mathbb{E}[Y_i(1) | D_i = 1] - \mathbb{E}[Y_i(0) | D_i = 0]\)
- ATCの識別条件
- \(\mathbb{E}[Y_i(1) | D_i = 1] = \mathbb{E}[Y_i(1) | D_i = 0]\)
- この場合、ATC = \(\mathbb{E}[Y_i(1) | D_i = 1] - \mathbb{E}[Y_i(0) | D_i = 0]\)
- これらは経験的に観察できず、理論的に説得する必要がある
- 前者の方が説得しやすいケースが多いので、ATTを推定するケースが多い
- 「もともと優秀な人が宋さんの授業を取る」と「授業の効果が高そうな人が宋さんの授業を取る」
その他のセレクションの例
手元のサンプルが「授業効果が高そうな学生(\(i \in \{1, 2, 4, 7, 8\}\))」だけなら…?
- 真の処置効果は0だが、この場合、処置効果は必ず正になる
- \(\Rightarrow\) 偏ったサンプリングによるバイアス(サンプルセレクション・バイアス)
| \(i\) | \(Y_i(0)\) | \(Y_i(1)\) | ITE |
|---|---|---|---|
| 1 | 500 | 550 | 50 |
| 2 | 200 | 300 | 100 |
| 3 | 800 | 750 | -50 |
| 4 | 300 | 400 | 100 |
| 5 | 300 | 200 | -100 |
| 6 | 550 | 450 | -100 |
| 7 | 700 | 750 | 50 |
| 8 | 400 | 600 | 200 |
| 9 | 500 | 300 | -200 |
| 10 | 600 | 550 | -50 |
| 平均 | 0 |
セレクションへの対処
- 無作為抽出(random sampling)
- サンプルセレクション・バイアス(サンプリング・バイアス)が存在する場合
- ランダム割り当て(無作為割当; random assignment)
- あらゆる内生性を(理論上)完全に除去できる因果推論の王道
- 統計的因果推論(statistical causal inference)
- 共変量調整
- 自然実験、疑似実験など
内生性