| ID | D | X | Y | Y(0) | Y(1) |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 2 |
| 2 | 0 | 0 | -1 | -1 | 1 |
| 3 | 0 | 0 | 1 | 1 | 3 |
| 4 | 1 | 0 | 4 | 2 | 4 |
| 5 | 1 | 0 | 5 | 3 | 5 |
| 6 | 1 | 0 | -1 | -3 | -1 |
| 7 | 1 | 0 | 0 | -2 | 0 |
| 8 | 1 | 0 | 1 | -1 | 1 |
| 9 | 1 | 0 | 2 | 0 | 2 |
| 10 | 1 | 0 | 3 | 1 | 3 |
| 11 | 0 | 1 | 4 | 4 | 6 |
| 12 | 0 | 1 | 5 | 5 | 7 |
| 13 | 0 | 1 | 1 | 1 | 3 |
| 14 | 0 | 1 | 0 | 0 | 2 |
| 15 | 0 | 1 | 2 | 2 | 4 |
| 16 | 0 | 1 | 3 | 3 | 5 |
| 17 | 0 | 1 | 6 | 6 | 8 |
| 18 | 1 | 1 | 4 | 2 | 4 |
| 19 | 1 | 1 | 5 | 3 | 5 |
| 20 | 1 | 1 | 6 | 4 | 6 |
社会科学における因果推論
5/ 回帰分析
1 回帰分析
単回帰分析
単回帰分析(simple regression):説明変数が1つのみの線形回帰分析
- \(Y\)を\(D\)に回帰する(regress \(Y\) on \(D\))
\[ \begin{eqnarray} Y_i & = & \mathbb{E}[Y_i|D_i] + \varepsilon_i & = & \alpha + \tau D_i + \varepsilon_i \\ \hat{Y}_i & = & \mathbb{E}[Y_i|D_i] & = & \hat{\alpha} + \hat{\tau} D_i \end{eqnarray} \]
- 推定対象:\(\hat{\alpha}\)、\(\hat{\tau}\)
- 推定方法:最小二乗法(ordinary least squares; OLS)
最小二乗法
- 残差の二乗和を最小とする\(\hat{\alpha}\)と\(\hat{\tau}\)を推定
- 残差(residuals):\(u_i = Y_i - \hat{Y}_i = Y_i - \hat{\alpha} - \hat{\tau} D_i\)
- \(u_i\)は\(\varepsilon_i\)の推定値(\(\hat{\varepsilon}\))
- 残差自乗和の平方根は「RMSE」(Root mean square error)とも呼ばれる
- 残差(residuals):\(u_i = Y_i - \hat{Y}_i = Y_i - \hat{\alpha} - \hat{\tau} D_i\)
\[ (\hat{\alpha}, \hat{\tau}) = \mathop{\arg \min}_{\alpha, \tau} \sum_{i}^{n}(Y_i - \alpha - \tau D_i)^2 \]
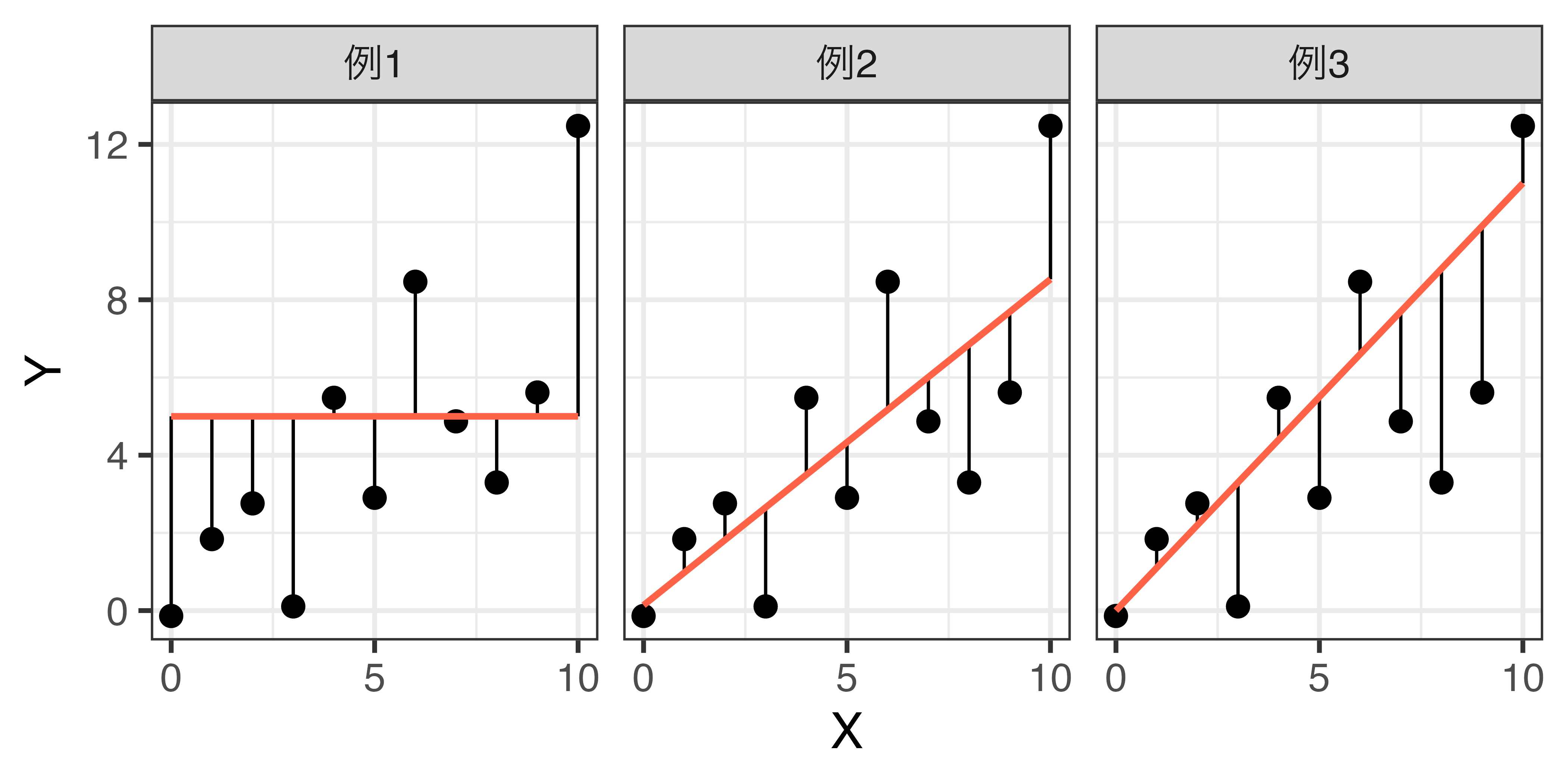
最小二乗法の例
- 残差の二乗和は141.13(左)、58.82(中)、66.55(右)
- RMSEはそれぞれ3.76、2.43、2.85
単回帰分析と因果推論
処置変数が外生変数、かつ二値変数なら\(D_i\)の係数の推定値はATEの推定値
- 処置変数\(D\)が二値変数の場合、\(\hat{\tau}\)は二群間の平均値の差分
- \(\hat{\tau}\) = ATT + セレクションバイアス
\[ \small \begin{align} \hat{\tau} & = \mathbb{E}[Y_i(1)|D_i = 1] - \mathbb{E}[Y_i(0)|D_i = 0] \\ & = \underbrace{\mathbb{E}[Y_i(1)|D_i = 1] - \mathbb{E}[Y_i(0)|D_i = 1]}_{\textsf{ATT}} + \underbrace{\mathbb{E}[Y_i(0)|D_i = 1] - \mathbb{E}[Y_i(0)|D_i = 0]}_{\textsf{selection bias}} \end{align} \]
- 処置変数が外生変数(=交換可能性/平均独立が成立)なら…12
\[ \hat{\tau} = \mathbb{E}[Y_i(1)] - \mathbb{E}[Y_i(0)] = \textsf{ATE} \]
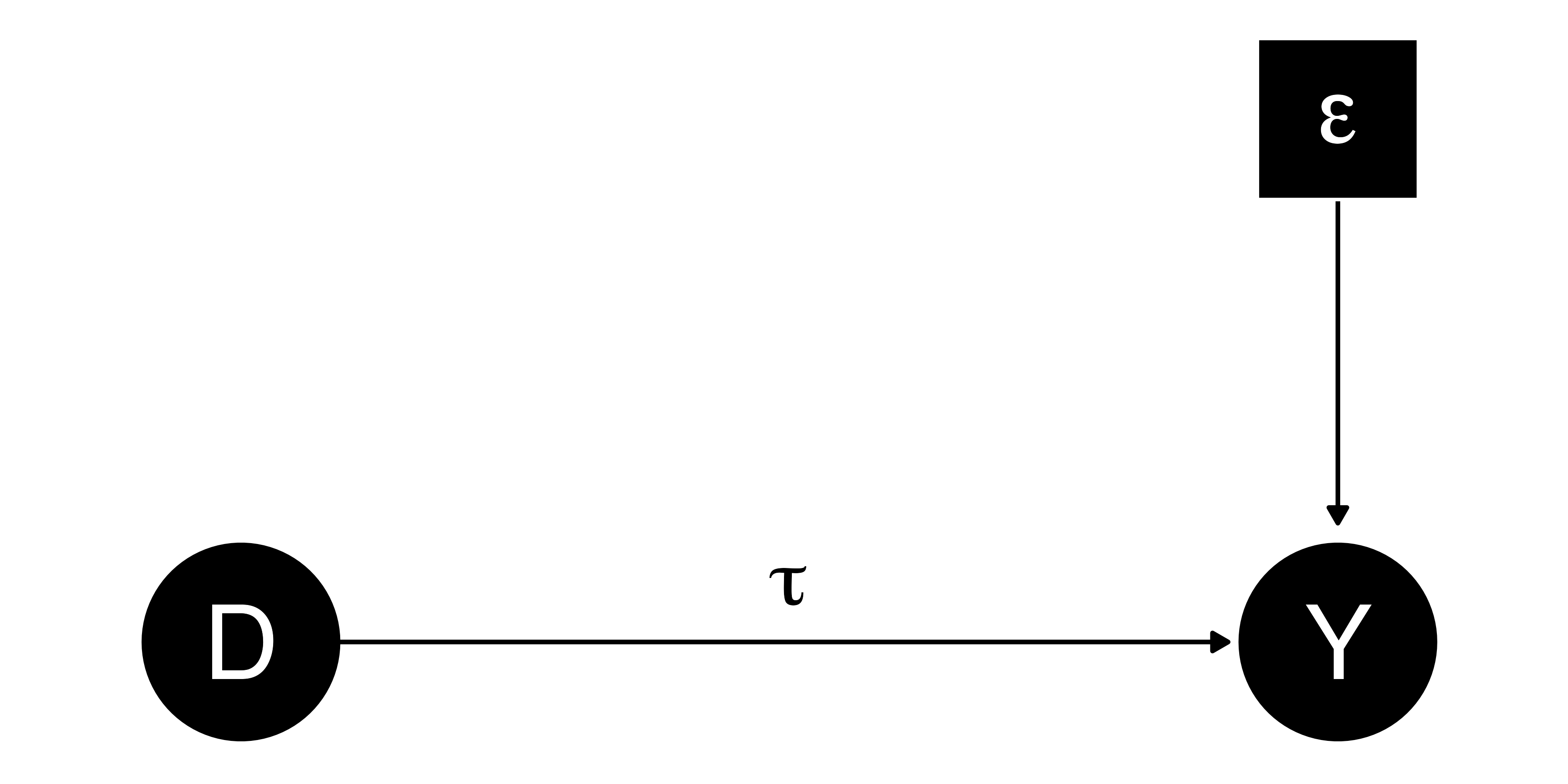
誤差に関する仮定
- 回帰分析における誤差の仮定
- 誤差の期待値は0(\(\mathbb{E}[\varepsilon_i]\) = 0)
- 誤差と説明変数は独立(\(\textsf{Cov}(D, \varepsilon)\) = \(\mathbb{E}[D \times \varepsilon]\) = 0)
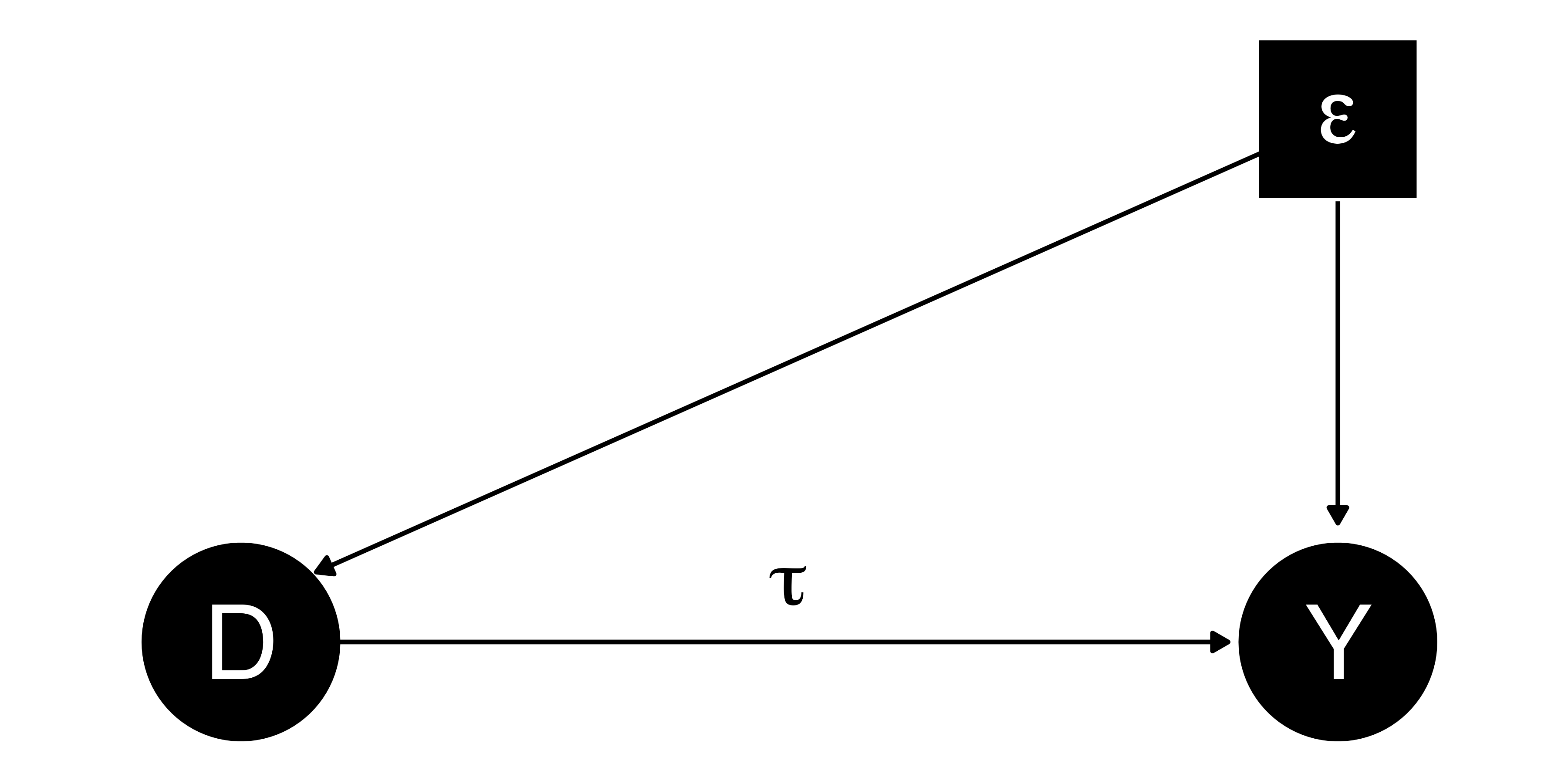
処置変数が内生変数の場合
- 誤差と説明変数は独立しない場合、\(\hat{\tau}\)はバイアス付きのATT
- \(\textsf{Cov}(D, \varepsilon) \neq\) 0
- \(\mathbb{E}[D \times \varepsilon] \neq\) 0
交絡要因が既知の場合
- 観察済みの変数\(X\)が唯一の交絡要因ある場合
- 単回帰分析では\(X\)は\(\varepsilon\)の一部だったが、\(X\)が観察済みなら\(\varepsilon \rightarrow X\)のパスを消せる
- そのためには、内生性の原因である\(X\)を考慮したモデリングが必要

重回帰分析
統制変数\(X\)を追加した回帰モデル
\[ \begin{align} Y_i & = \mathbb{E}[Y_i|D_i, X_i] + \varepsilon_i \\ & = \alpha + \tau D_i + \beta X_i + \varepsilon_i \end{align} \]
- 残差の二乗和を最小とする\(\hat{\alpha}\)と\(\hat{\tau}\)、\(\hat{\beta}\)を推定
- 残差(residuals):\(Y_i - \alpha - \tau D_i - \beta X_i\)
\[ (\hat{\alpha}, \hat{\tau}, \hat{\beta}) = \mathop{\arg \min}_{\alpha, \tau, \beta} \sum_{i}^{n}(Y_i - \alpha - \tau D_i - \beta X_i)^2 \]
統制変数の役割
\(X_i = x\)における傾き(\(\tau\))の推定
- ただし、\(X_i = x\)における傾きと\(X_i = x^{\prime}\)における傾きは同じと仮定1(\(x \neq x^{\prime}\))
統制変数とブロッキング
重回帰分析における係数は通常、「他の変数が一定であれば…」と解釈される。
- \(\Rightarrow\) 重回帰分析の推定値 = ブロック内処置効果の加重平均
手順
- ブロックごとに処置効果(A)を推定する
- (A)の加重平均を計算する。各ブロックの重みは、
- \(Pr(X_i = x)\)(ATEを推定する場合)
- \(Pr(X_i = x, D_i = 1)\)(ATTを推定する場合)
- \(Pr(X_i = x, D_i = 0)\)(ATCを推定する場合)
- \(\Rightarrow\) 統制変数をうまく使えば因果推論ができそう
- どうすれば回帰分析で信頼できる処置効果が推定できるか
- \(\Rightarrow\) ブロック内で処置群と統制群が交換可能(or 平均独立)であれば…?
2 仮定
条件付き独立の仮定
条件付き独立の仮定(conditional independence assumption; CIA)
- 統制変数(X)で条件づけた場合、処置変数(D)と結果変数(Y)の潜在的結果は独立する
- 条件付き独立 = 条件付き交換可能性 = 条件付き無視可能性
\[ \{Y(0), Y(1)\} \mathop{\perp\!\!\!\!\perp} D | X \]
- 全体では交換可能性が成立しないものの、統制変数Xで条件づけた下位グループ内では交換可能性が成立
- 観察データを用いた回帰分析で因果推論を行うための仮定
条件付き平均独立性
CIAが成立すると条件付き平均独立性が成り立つ
- 平均独立性が成り立つとATEが推定可能となる
\[ \mathbb{E}[Y_i(1)|D_i = 1, X_i = x] = \mathbb{E}[Y_i(1)|D_i = 0, X_i = x] = \mathbb{E}[Y_i(1)|X_i = x] \]
\[ \mathbb{E}[Y_i(0)|D_i = 1, X_i = x] = \mathbb{E}[Y_i(0)|D_i = 0, X_i = x] = \mathbb{E}[Y_i(0)|X_i = x] \]
条件付き平均独立の例
真のATE
\[ \underbrace{\mathbb{E}[Y_i(1)]}_{\textsf{3.5}} - \underbrace{\mathbb{E}[Y_i(0)]}_{\textsf{1.5}} = 2 \]
ATEの推定値
Difference-in-means(DiM)推定量
\[ \underbrace{\mathbb{E}[Y_i|D_i = 1]}_{\textsf{2.9}} - \underbrace{\mathbb{E}[Y_i|D_i = 0]}_{\textsf{2.1}} = 0.8 \]
平均独立性は成立するか
| ID | D | X | Y | Y(0) | Y(1) |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 2 |
| 2 | 0 | 0 | -1 | -1 | 1 |
| 3 | 0 | 0 | 1 | 1 | 3 |
| 4 | 1 | 0 | 4 | 2 | 4 |
| 5 | 1 | 0 | 5 | 3 | 5 |
| 6 | 1 | 0 | -1 | -3 | -1 |
| 7 | 1 | 0 | 0 | -2 | 0 |
| 8 | 1 | 0 | 1 | -1 | 1 |
| 9 | 1 | 0 | 2 | 0 | 2 |
| 10 | 1 | 0 | 3 | 1 | 3 |
| 11 | 0 | 1 | 4 | 4 | 6 |
| 12 | 0 | 1 | 5 | 5 | 7 |
| 13 | 0 | 1 | 1 | 1 | 3 |
| 14 | 0 | 1 | 0 | 0 | 2 |
| 15 | 0 | 1 | 2 | 2 | 4 |
| 16 | 0 | 1 | 3 | 3 | 5 |
| 17 | 0 | 1 | 6 | 6 | 8 |
| 18 | 1 | 1 | 4 | 2 | 4 |
| 19 | 1 | 1 | 5 | 3 | 5 |
| 20 | 1 | 1 | 6 | 4 | 6 |
| \(\mathbb{E}[Y_i(0)|D_i]\) | \(\mathbb{E}[Y_i(1)|D_i]\) | |
|---|---|---|
| \(D_i = 0\) | 2.1 | 4.1 |
| \(D_i = 1\) | 0.9 | 2.9 |
ケース1:平均独立性\(\times\)
- もし、現在の処置群が統制群になったら…
- \(\mathbb{E}[Y_i(0)|D_i = 1]\) = 0.9
- もし、現在の統制群が統制群になったら…(観察済)
- \(\mathbb{E}[Y_i(0)|D_i = 0]\) = 2.1
ケース2:平均独立性\(\times\)
- もし、現在の処置群が処置群になったら…(観察済)
- \(\mathbb{E}[Y_i(1)|D_i = 1]\) = 2.9
- もし、現在の統制群が処置群になったら…
- \(\mathbb{E}[Y_i(1)|D_i = 0]\) = 4.1
\(X_i = 0\)の場合
| ID | D | X | Y | Y(0) | Y(1) |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 2 |
| 2 | 0 | 0 | -1 | -1 | 1 |
| 3 | 0 | 0 | 1 | 1 | 3 |
| 4 | 1 | 0 | 4 | 2 | 4 |
| 5 | 1 | 0 | 5 | 3 | 5 |
| 6 | 1 | 0 | -1 | -3 | -1 |
| 7 | 1 | 0 | 0 | -2 | 0 |
| 8 | 1 | 0 | 1 | -1 | 1 |
| 9 | 1 | 0 | 2 | 0 | 2 |
| 10 | 1 | 0 | 3 | 1 | 3 |
| \(\mathbb{E}[Y_i(0)|D_i, X_i = 0]\) | \(\mathbb{E}[Y_i(1)|D_i, X_i = 0]\) | |
|---|---|---|
| \(D_i = 0\) | 0.0 | 2.0 |
| \(D_i = 1\) | 0.0 | 2.0 |
ケース1:平均独立性\(\bigcirc\)
- もし、現在の処置群が統制群になったら…
- \(\mathbb{E}[Y_i(0)|D_i = 1]\) = 0
- もし、現在の統制群が統制群になったら…(観察済)
- \(\mathbb{E}[Y_i(0)|D_i = 0]\) = 0
ケース2:平均独立性\(\bigcirc\)
- もし、現在の処置群が処置群になったら…(観察済)
- \(\mathbb{E}[Y_i(1)|D_i = 1]\) = 2
- もし、現在の統制群が処置群になったら…
- \(\mathbb{E}[Y_i(1)|D_i = 0]\) = 2
\(X_i = 1\)の場合
| ID | D | X | Y | Y(0) | Y(1) |
|---|---|---|---|---|---|
| 11 | 0 | 1 | 4 | 4 | 6 |
| 12 | 0 | 1 | 5 | 5 | 7 |
| 13 | 0 | 1 | 1 | 1 | 3 |
| 14 | 0 | 1 | 0 | 0 | 2 |
| 15 | 0 | 1 | 2 | 2 | 4 |
| 16 | 0 | 1 | 3 | 3 | 5 |
| 17 | 0 | 1 | 6 | 6 | 8 |
| 18 | 1 | 1 | 4 | 2 | 4 |
| 19 | 1 | 1 | 5 | 3 | 5 |
| 20 | 1 | 1 | 6 | 4 | 6 |
| \(\mathbb{E}[Y_i(0)|D_i, X_i = 1]\) | \(\mathbb{E}[Y_i(1)|D_i, X_i = 1]\) | |
|---|---|---|
| \(D_i = 0\) | 3.0 | 5.0 |
| \(D_i = 1\) | 3.0 | 5.0 |
ケース1:平均独立性\(\bigcirc\)
- もし、現在の処置群が統制群になったら…
- \(\mathbb{E}[Y_i(0)|D_i = 1]\) = 3
- もし、現在の統制群が統制群になったら…(観察済)
- \(\mathbb{E}[Y_i(0)|D_i = 0]\) = 3
ケース2:平均独立性\(\bigcirc\)
- もし、現在の処置群が処置群になったら…(観察済)
- \(\mathbb{E}[Y_i(1)|D_i = 1]\) = 5
- もし、現在の統制群が処置群になったら…
- \(\mathbb{E}[Y_i(1)|D_i = 0]\) = 5
条件付き平均独立と回帰分析
条件付き平均独立が成立する場合、重回帰分析でバイアスのないATEが推定可能
- CIAが成り立ったらさらに良い
| 統制変数なし | 統制変数あり | |
|---|---|---|
| 注:カッコ内はHC2頑健標準誤差 | ||
| 切片 | 2.100 (0.737) | -0.000 (0.560) |
| D | 0.800 (1.042) | 2.000 (0.683) |
| X | 3.000 (0.683) | |
| Num.Obs. | 20 | 20 |
| R2 | 0.032 | 0.406 |
- 統制変数なし(単回帰分析)のATEの推定値:0.8
- 処置群と統制群を交換する場合、ATEの推定値は3.2
- 統制変数あり(重回帰分析)のATEの推定値:2.0
- {\(X_i = 0\)におけるATE} = {\(X_i = 1\)におけるATE} = 2
- \(X_i = x\)で処置群と統制群を交換してもATEの推定値は2
CIA/条件付き平均独立性は確認可能か
条件付き平均独立性
\[ \mathbb{E}[Y_i(1)|D_i = 1, X_i = x] = \mathbb{E}[Y_i(1)|D_i = 0, X_i = x] = \mathbb{E}[Y_i(1)|X_i = x] \]
\[ \mathbb{E}[Y_i(0)|D_i = 1, X_i = x] = \mathbb{E}[Y_i(0)|D_i = 0, X_i = x] = \mathbb{E}[Y_i(0)|X_i = x] \]
- \(\mathbb{E}[Y_i(1)|D_i = 0, X_i = x]\)、\(\mathbb{E}[Y_i(0)|D_i = 1, X_i = x]\)は観察不可
- \(\Rightarrow\) 平均独立性が成り立っているかどうかは確認できない
- 平均独立性よりも厳しいCIAの確認はさらに難しい
- 「Xで条件付ければ平均独立性が成り立つだろう」と仮定するしかない
- 非実験データであれば、変数選択&モデリングを慎重に行う必要がある
- \(\Rightarrow\) 平均独立性が成り立っているかどうかは確認できない
- もし、間違った条件付けをしてしまったら…?
3 欠落変数バイアス
欠落変数バイアスの定式化
- 3つのモデル(真の処置効果は\(\tau^l\))
- 真のモデル(long regression):\(Y_i = \alpha^l + \tau^l D_i + \beta^l X_i + \varepsilon_i\)
- バイアス付きのモデル(short regression):\(Y_i = \alpha^s + \tau^s D_i + \zeta_i\)
- XをDに回帰したモデル:\(X_i = \alpha_0 + \lambda D_i + \nu_i\)
真のモデルからXが消えたら…
\[ \begin{align} Y_i & = \alpha^l + \tau^l D_i + \beta^l X_i + \varepsilon_i \\ & = \alpha^l + \tau^l D_i + \beta^l (\alpha_0 + \lambda D_i + \nu_i) + \varepsilon_i \\ & = \alpha^l + \tau^l D_i + \beta^l\alpha_0 + \beta^l \lambda D_i + \beta^l \nu_i + \varepsilon_i \\ & = \underbrace{(\alpha^l + \beta^l\alpha_0)}_{\alpha^s} + \underbrace{(\tau^l + \beta^l \lambda)}_{\tau^s} D_i + \underbrace{(\varepsilon_i + \beta^l \nu_i)}_{\varepsilon_i} \end{align} \]
欠落変数バイアス
欠落変数バイアス(omitted variable bias; OVB)
- \(\beta^l\):X \(\rightarrow\) Yの係数
- \(\lambda\):D \(\rightarrow\) Xの係数
\[ \underbrace{\tau^s}_{\textsf{バイアス付きの推定値}} = \underbrace{\tau^l}_{\textsf{真の処置効果}} + \underbrace{\textcolor{red}{\beta^l \lambda}}_{\textsf{欠落変数バイアス}} \]
- \(\beta^l = 0\)、または\(\lambda = 0\)ならOVBは発生しない
- \(\beta^l \neq 0\)、かつ\(\lambda \neq 0\)の場合、Xは交絡要因(confounder)である。
- 交絡要因を統制しないと、OVBが発生する
欠落変数バイアスの可視化(1)
職業訓練(D)は将来の年収(Y)にどのような影響を与えるか
- 負の効果?効果なし?内生性(自己選択)は?

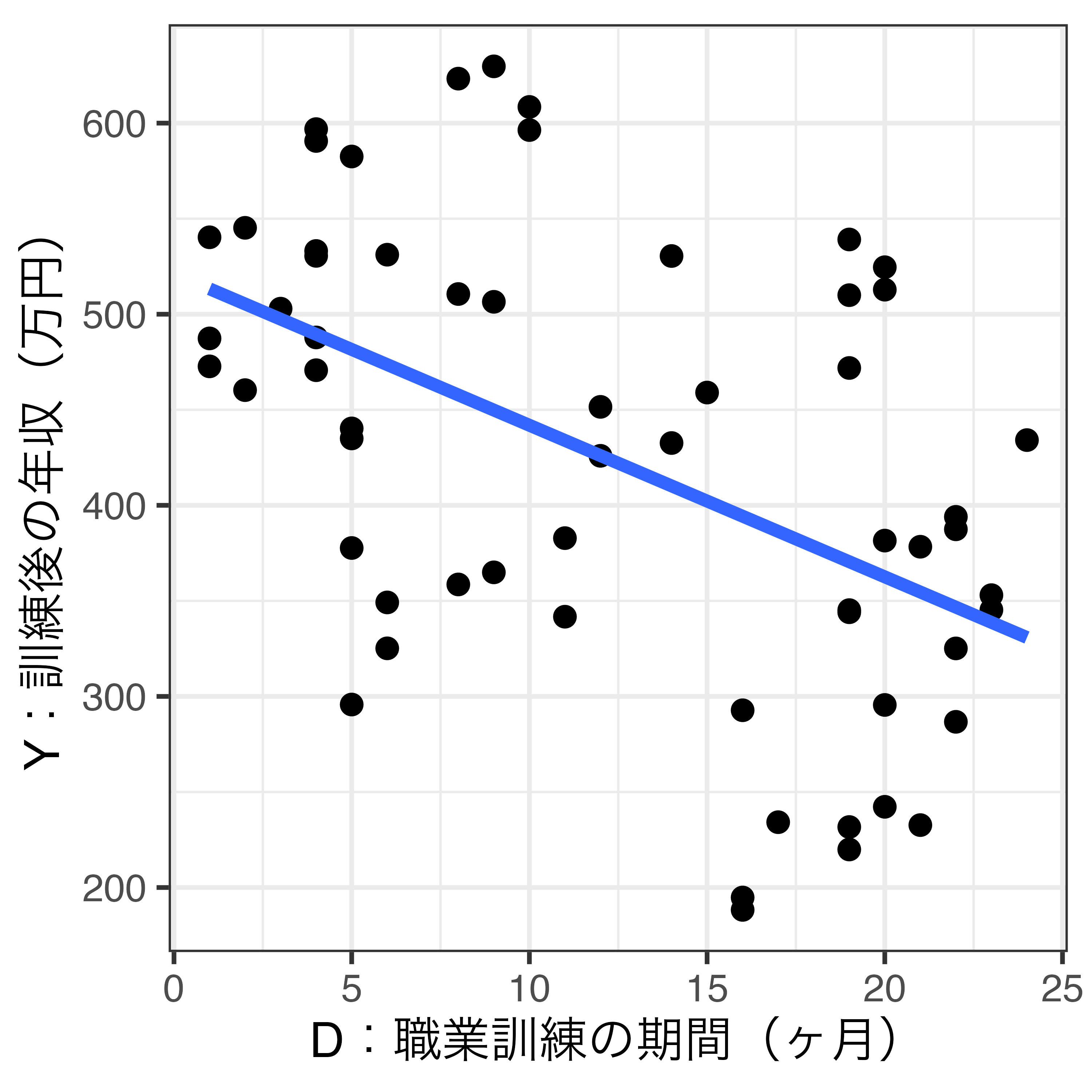
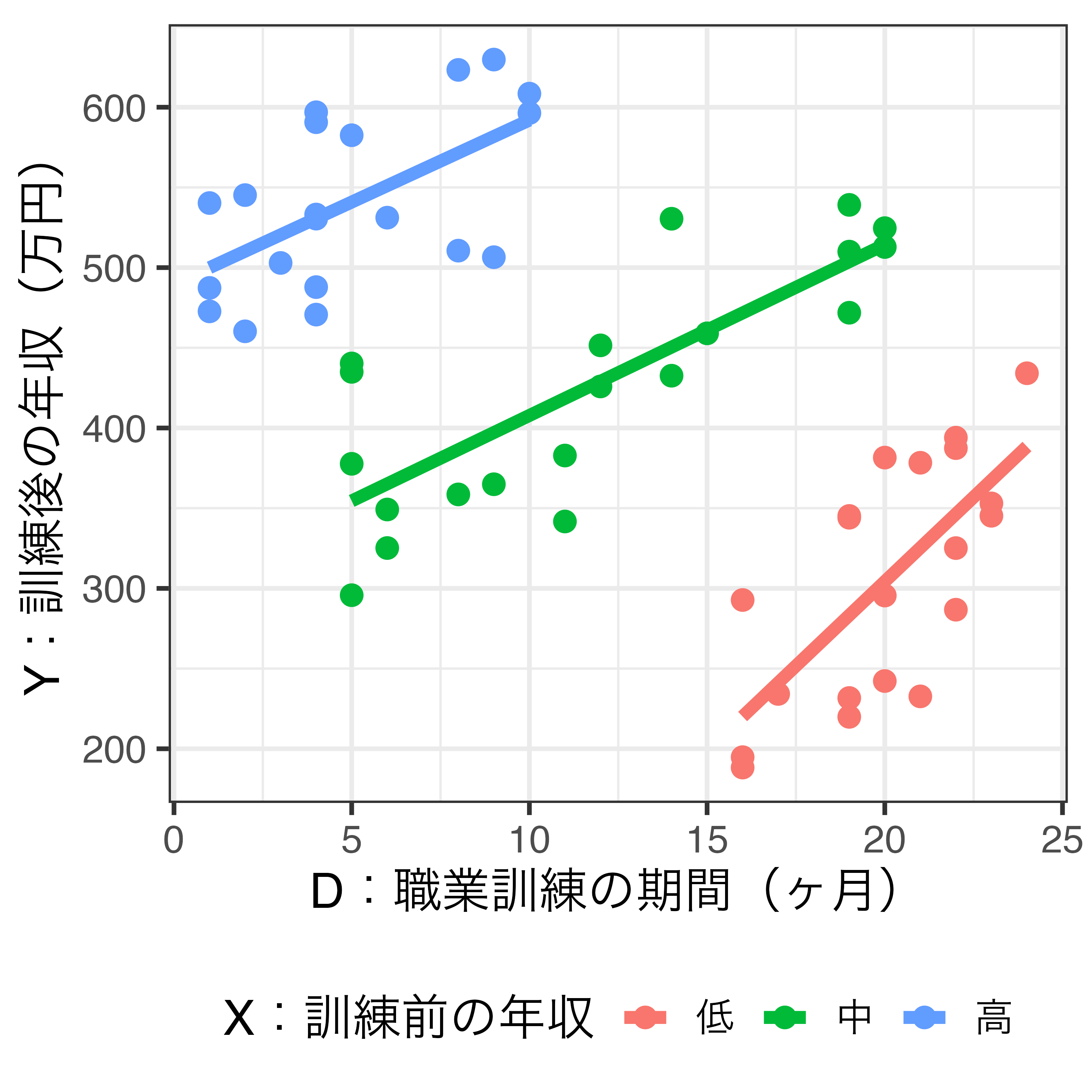
欠落変数バイアスの可視化(2)
交絡要因として職業訓練前の年収(X)
- 職業訓練前の年収を考慮したモデル:実は正の効果があるかも?
4 処置後変数バイアス
処置後変数とは
処置後変数(post-treatment variable)
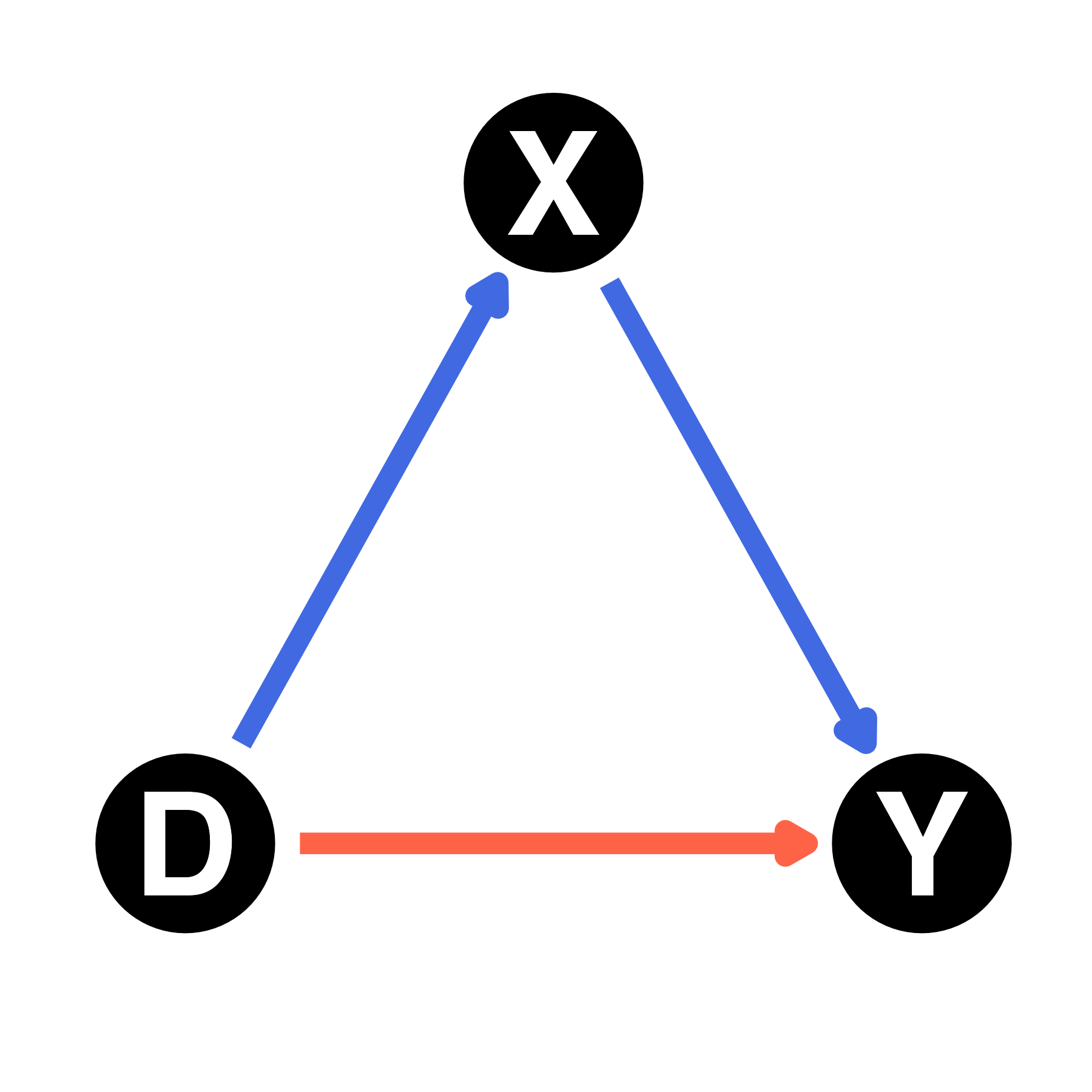
- XはDの処置後変数
- DがYに直接与える処置効果(直接効果)
- DがXを経由してYに与える処置効果(間接効果)
- 総効果 = 直接効果 + 間接効果
- 因果推論において主に注目するのは総効果
- この場合、Xを統制してはいけない
- 説明変数がDのみの単回帰分析を採用すべき
直接効果、間接効果、総効果
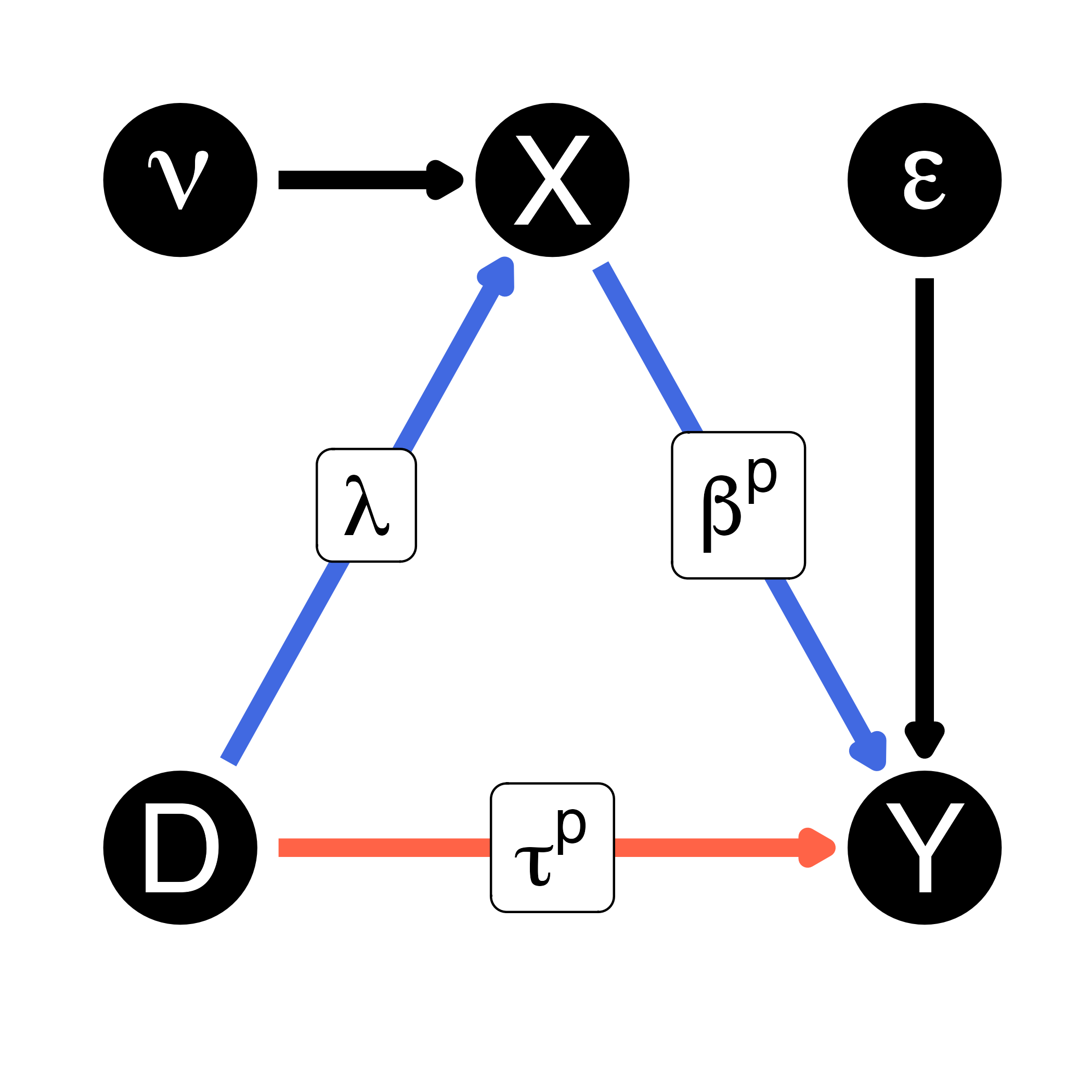
- 直接効果:\(\tau^p\)
- 間接効果:\(\lambda \times \beta^p\)
- Dが1単位上がると、Xが\(\lambda\)分増加するため
- 総効果:\(\tau^p + \lambda \beta^p\)
- \(\hat{y} = \beta_0 + \beta_1 D + \beta_2 X\)のモデル
- \(\beta_1\):直接効果(\(\tau^p\))
- \(\beta_2\):間接効果の一部(\(\beta^p\))
- \(\hat{y} = \beta_0 + \beta_1 D\)のモデル
- \(\beta_1\):総効果(\(\tau^p + \lambda \beta^p\))
処置後変数バイアスの数式化
- \(Y_i = \alpha^p + \tau^p D_i + \beta^p X_i + \varepsilon_i^p\)
- \(X_i = \alpha_0 + \lambda D_i + \nu_i\)
\[ \begin{align} Y_i & = \alpha^p + \tau^p D_i + \beta^p X_i + \varepsilon_i^p \\ & = \alpha^p + \tau^p D_i + \beta^p (\alpha_0 + \lambda D_i + \nu_i) + \varepsilon_i^p \\ & = \alpha^p + \tau^p D_i + \beta^p \alpha_0 + \beta^p \lambda D_i + \beta^p \nu_i + \varepsilon_i^p \\ & = (\alpha^p + \beta^p \alpha_0) + \textcolor{red}{(\tau^p + \beta^p \lambda)} D_i + (\beta^p \nu_i + \varepsilon_i^p) \end{align} \]
- YをDのみに回帰した場合の処置効果:\(\tau^p + \beta^p \lambda\)(=真の処置効果)
- Xがモデル含まれている場合の処置効果の推定値:\(\tau^p\)
- 処置後変数バイアス:\(-\beta^p \lambda\)
- \(\lambda\)か\(\beta^p\)が0なら、処置後変数バイアスは発生しない
- \(\lambda\) = 0なら、そもそもXはDの処置後変数ではない
5 変数選択
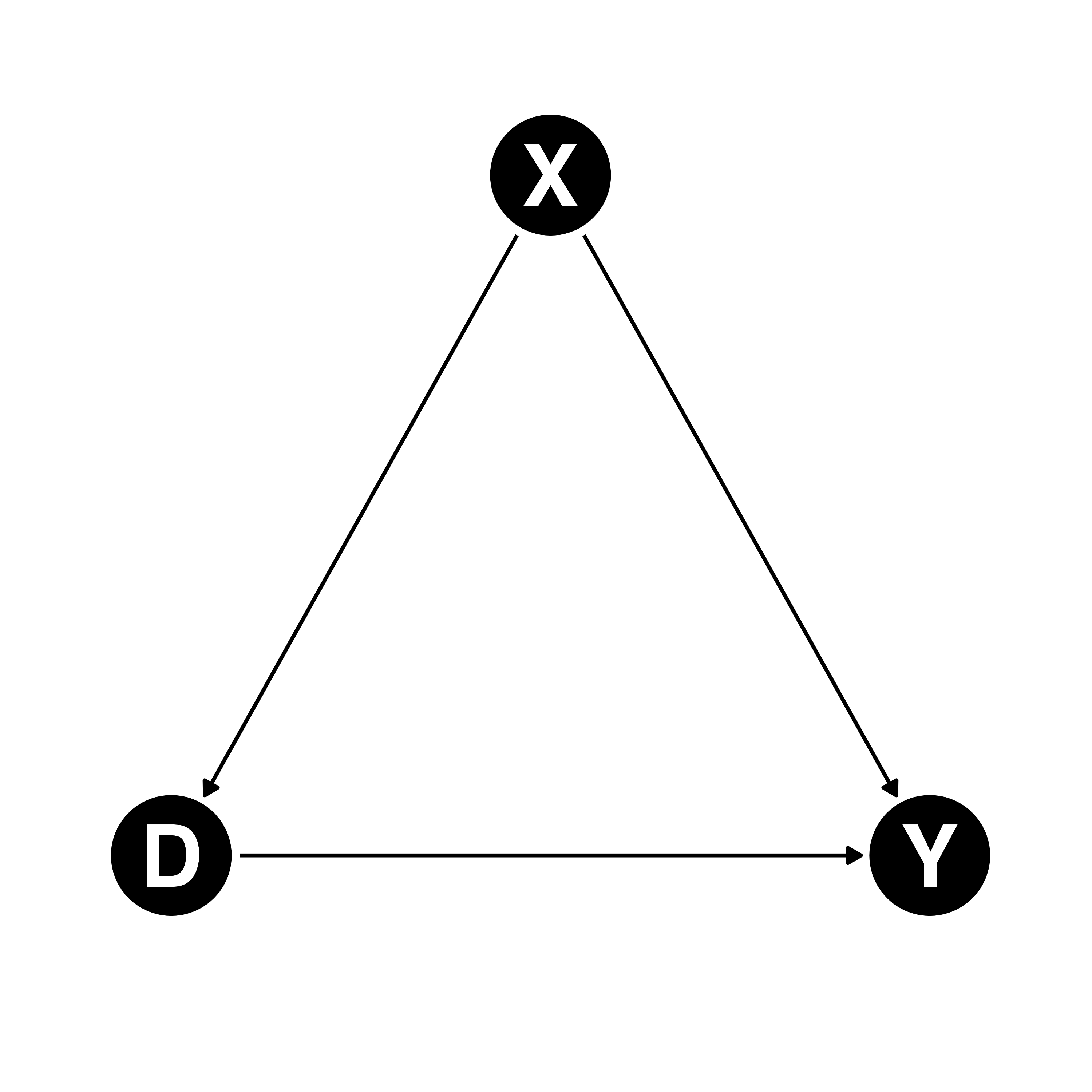
DAG
有向非巡回グラフ(Directed acyclic graph, DAG)
- サイクルが存在しない有向グラフ(無向グラフは常にサイクルが存在)
- 右グラフはサイクルが存在(D \(\rightarrow\) Y \(\rightarrow\) X \(\rightarrow\) D \(\rightarrow\) Y \(\rightarrow\)…)
- ノード(点; node or vertex)とエッジ(線; edge)で構成
- 因果推論での活用(詳細はPearl et al. [2016=2019]などを参照)


バックドア経路
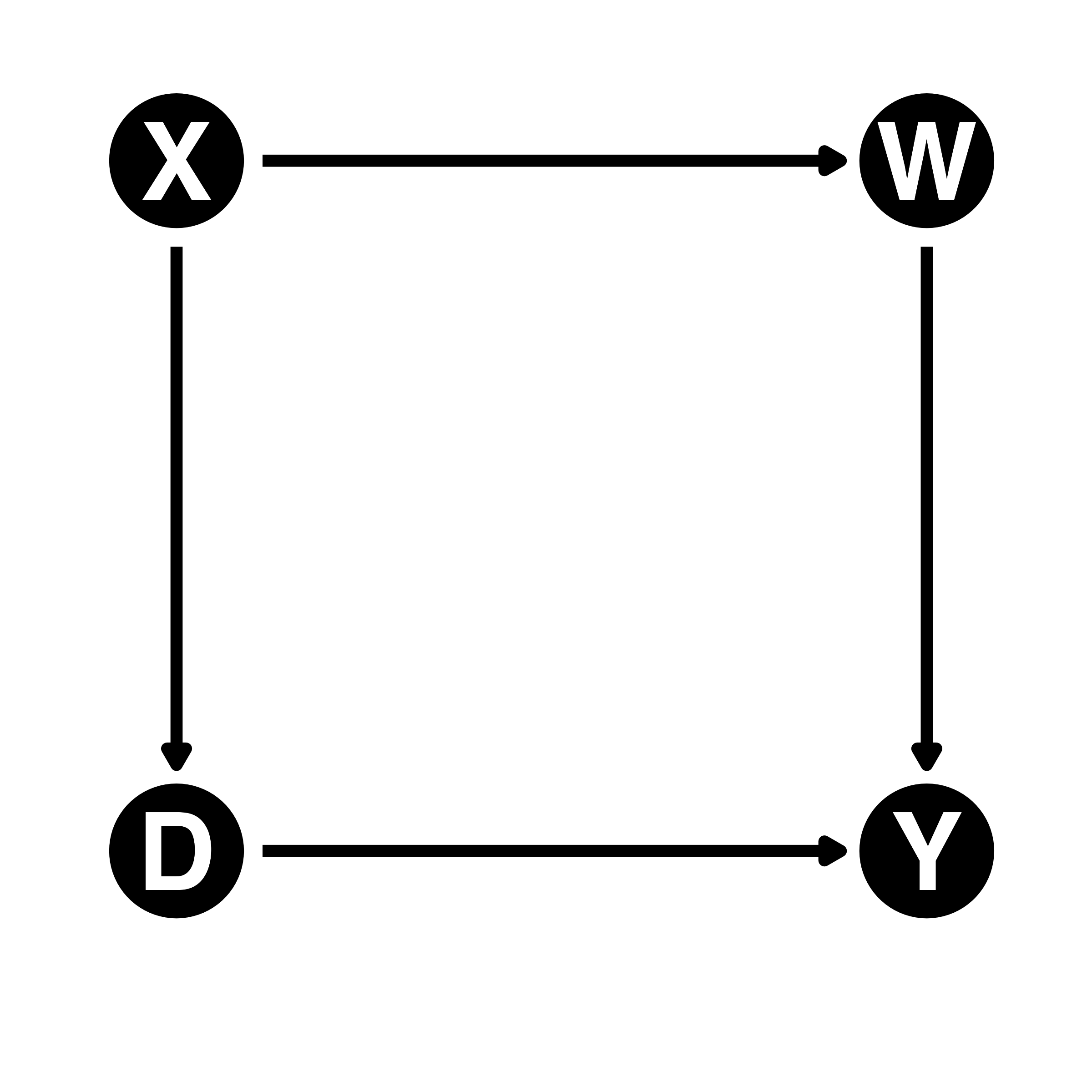
バックドア経路(backdoor path):原因と結果(DとY)間のすべての経路中、原因(D)へ向かう矢印を含む経路
- ただし、\(D \rightarrow Y\)のパスを除く
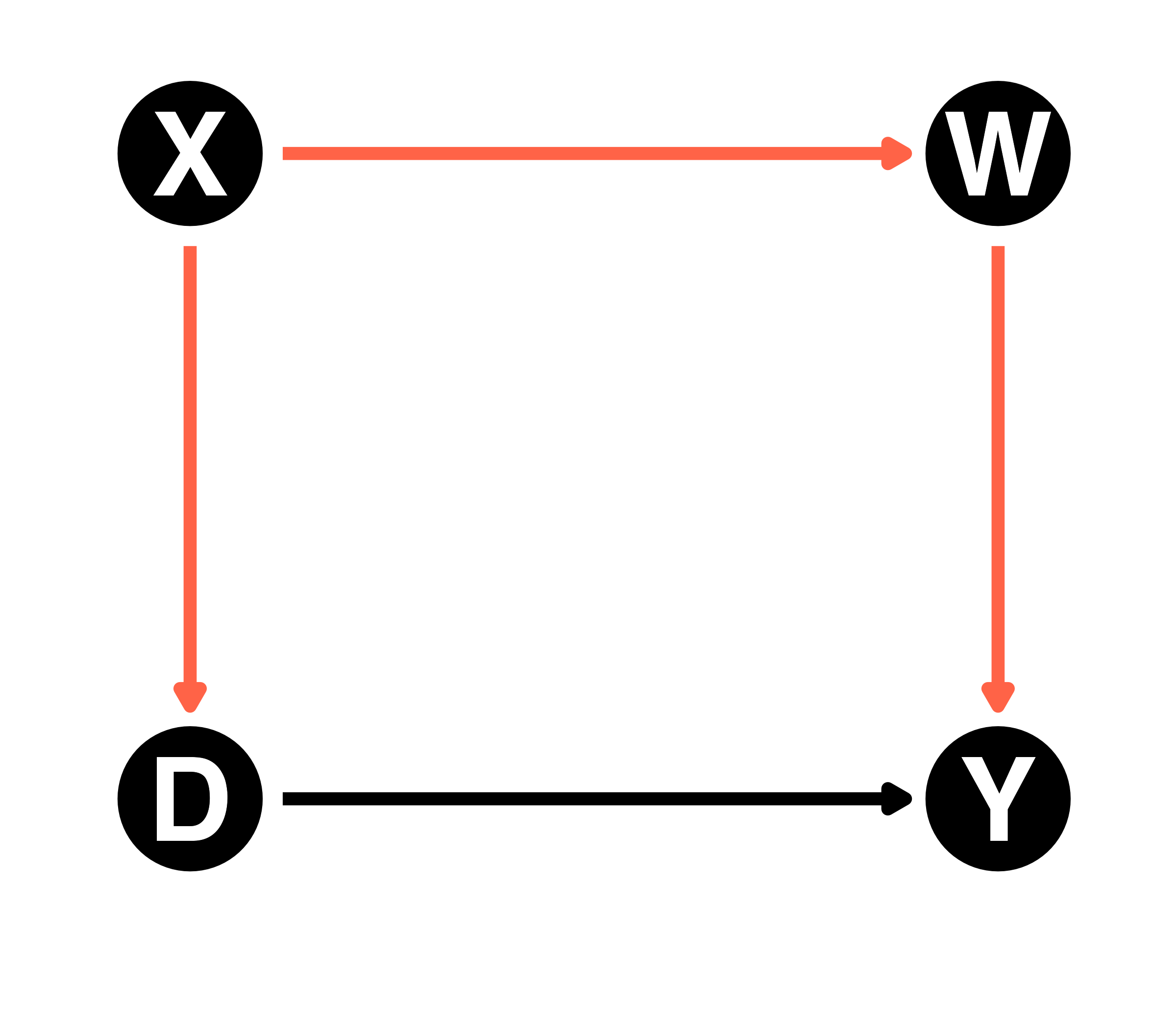
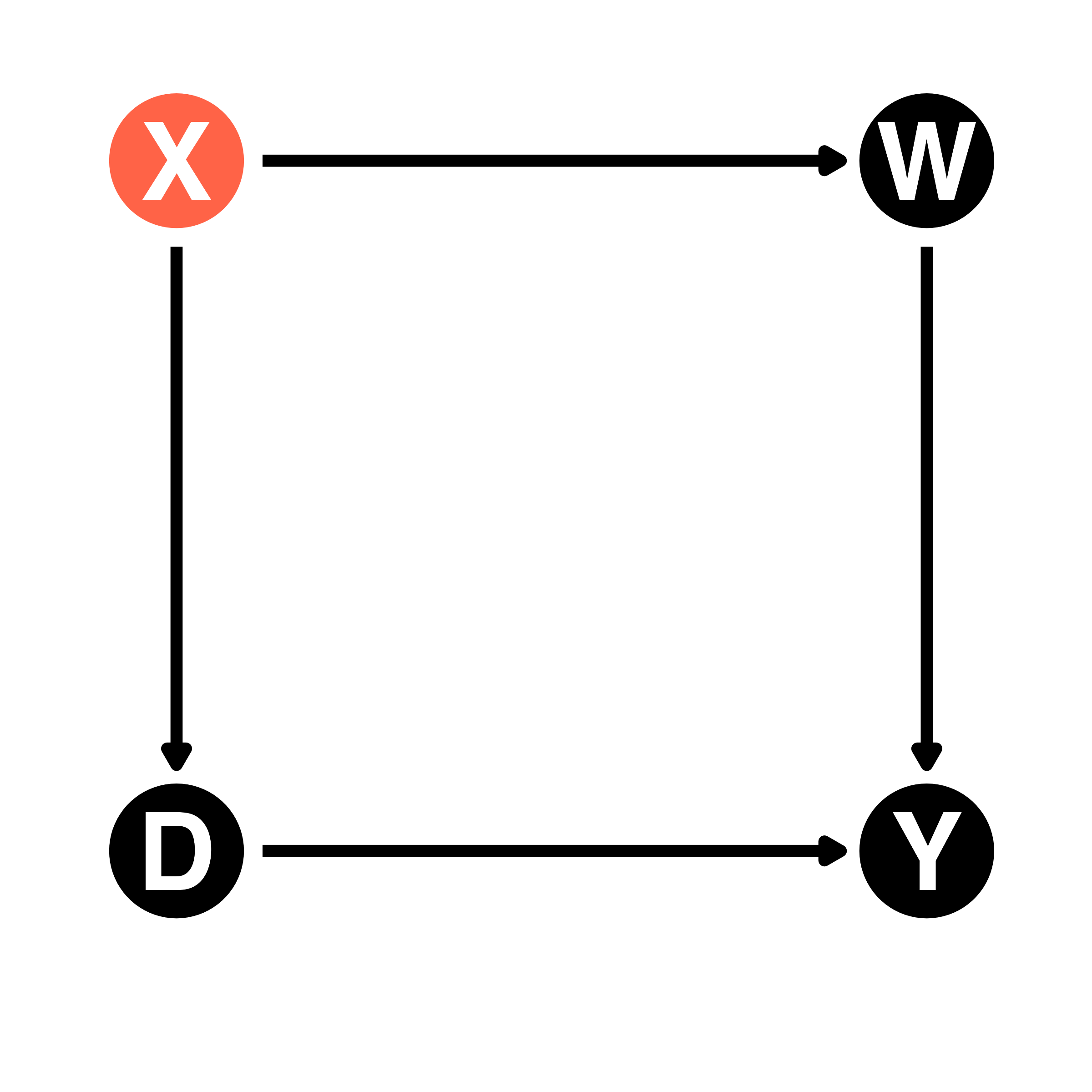
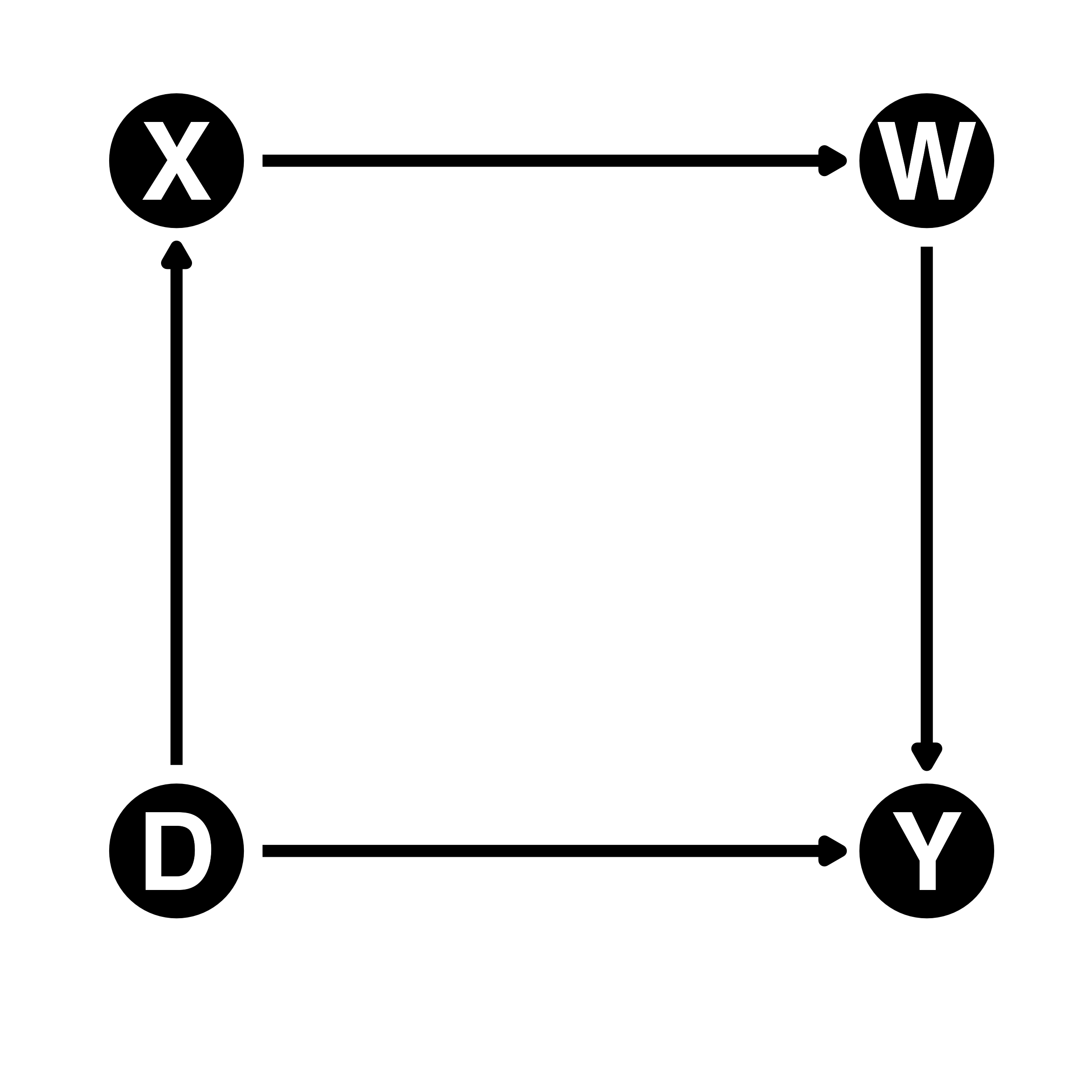
- 左:バックドア経路が存在(D \(\leftarrow\) X \(\rightarrow\) W \(\rightarrow\) Y)
- 右:バックドア経路が存在しない
- D \(\rightarrow\) X \(\rightarrow\) W \(\rightarrow\) YはDへ向かう矢印を含まない
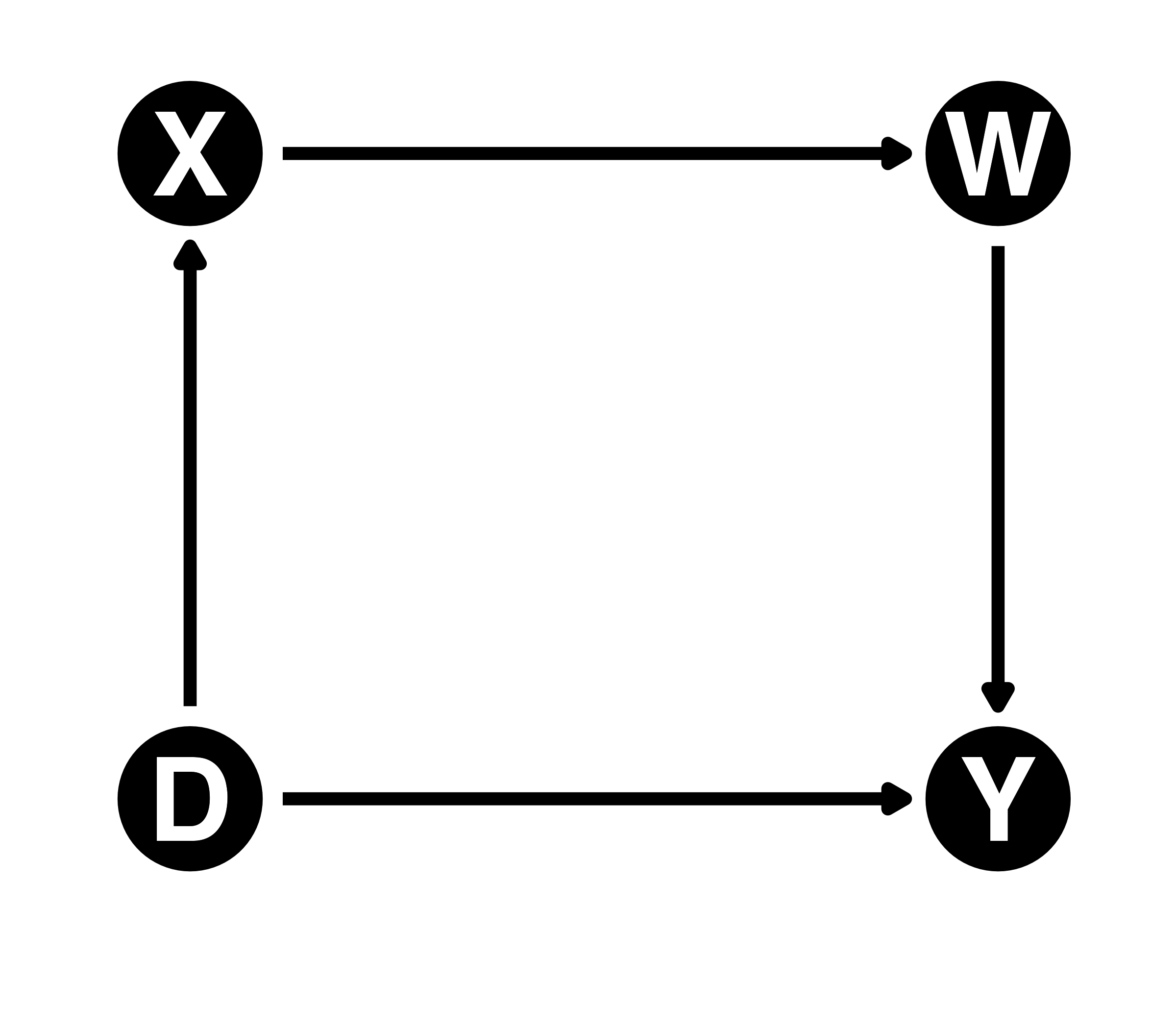
分岐点
分岐点(confounder):原因(D)と結果(Y)両方にたどり着ける変数
- バックドア経路に分岐点が存在するとそのバックドア経路は「開いている」
- 左:開いたバックドア経路がある(D \(\leftarrow\) X \(\rightarrow\) W \(\rightarrow\) Y)
- 右:分岐点が存在しない
分岐点への対処
バックドア経路が開いている場合、バックドア経路上の変数をモデルに投入するとバックドア経路は閉ざされる
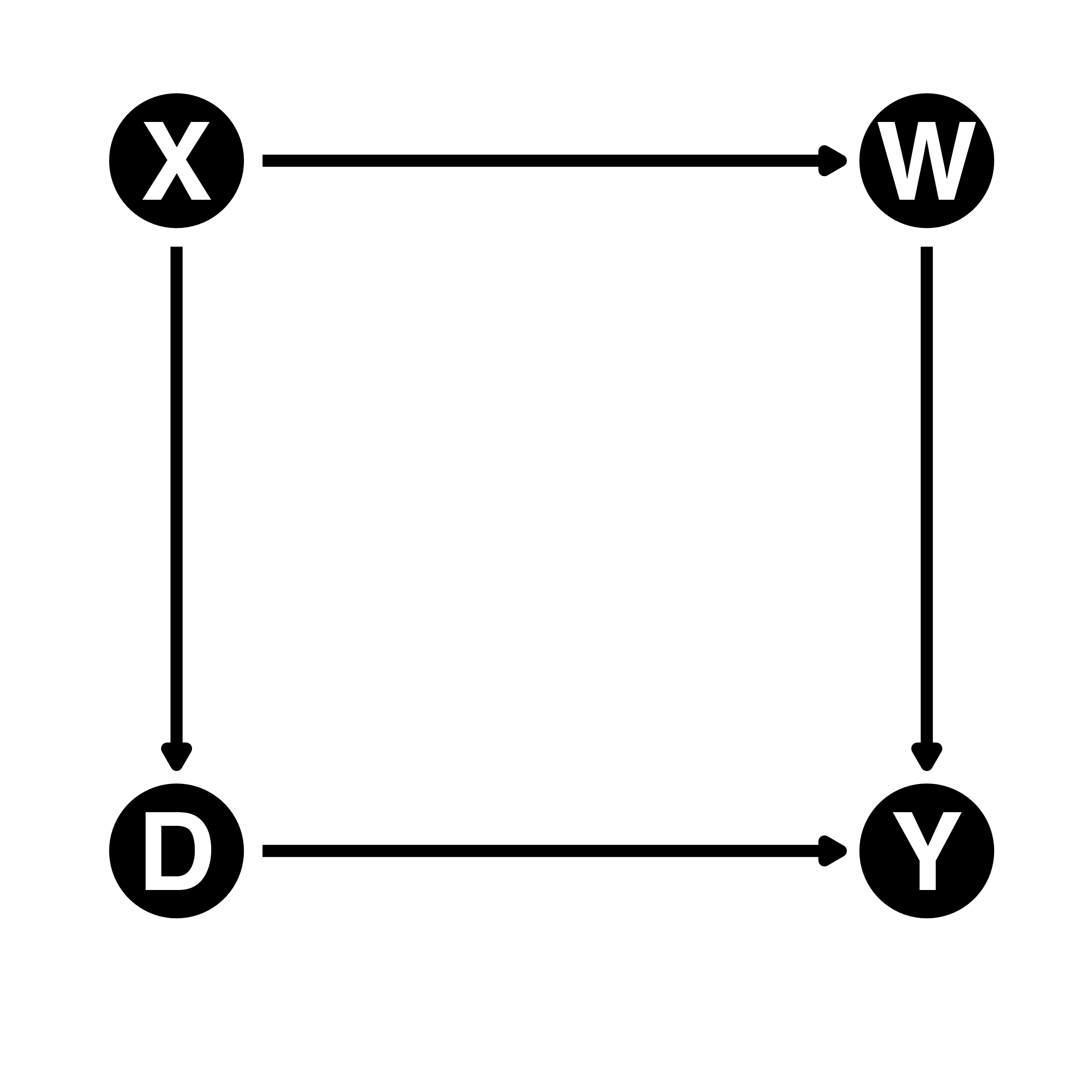
- 経路上の全変数を統制する必要はない
- バックドア経路さえ無くせば良い
- 経路上のすべての変数がなくても良い
- どのモデルでも\(\bigcirc\)
- Xのみ統制
- Wのみ統制
- XとW両方統制
- バックドア経路が開いたままだと、欠落変数バイアスが発生
合流点
合流点(collider):原因(D)と結果(Y)両方からたどり着ける変数
- バックドア経路に合流点が存在するとそのバックドア経路は「閉じている」
- 左:バックドア経路が開いている(D \(\leftarrow\) X \(\rightarrow\) W \(\rightarrow\) Y)
- 右:バックドア経路が閉じている(経路上に合流点が存在する; D \(\rightarrow\) X \(\rightarrow\) W \(\leftarrow\) Y)

中間点(要検討)
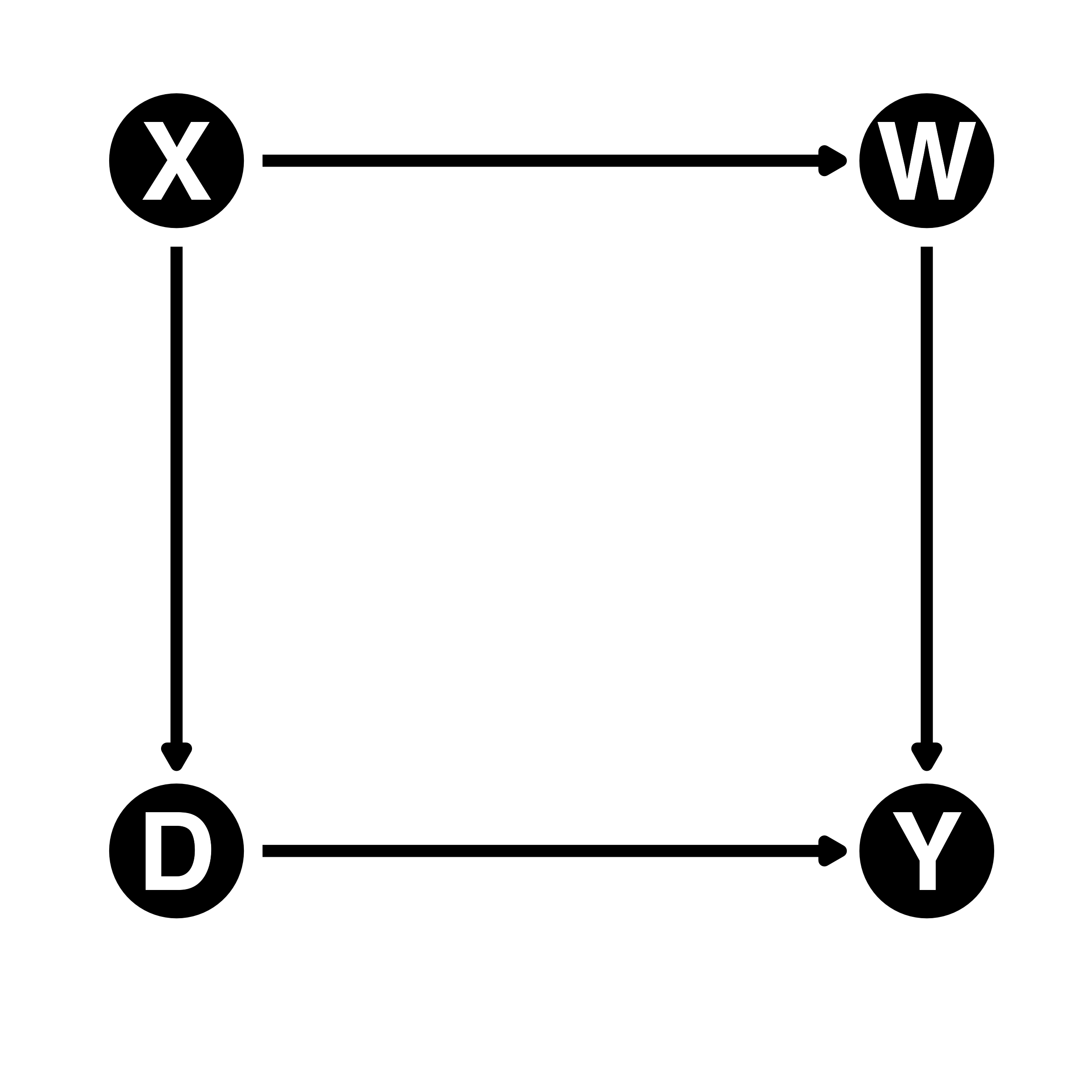
中間点(mediator):原因(D)から結果(Y)へ向かう経路上に存在する変数
- バックドア経路に中間点が存在するとそのバックドア経路は「閉じている」
- 左:バックドア経路が開いている(D \(\leftarrow\) X \(\rightarrow\) W \(\rightarrow\) Y)
- 右:バックドア経路が閉じている(経路上に中間点が存在する; D \(\rightarrow\) X \(\rightarrow\) W \(\rightarrow\) Y)
合流点・中間点への対処
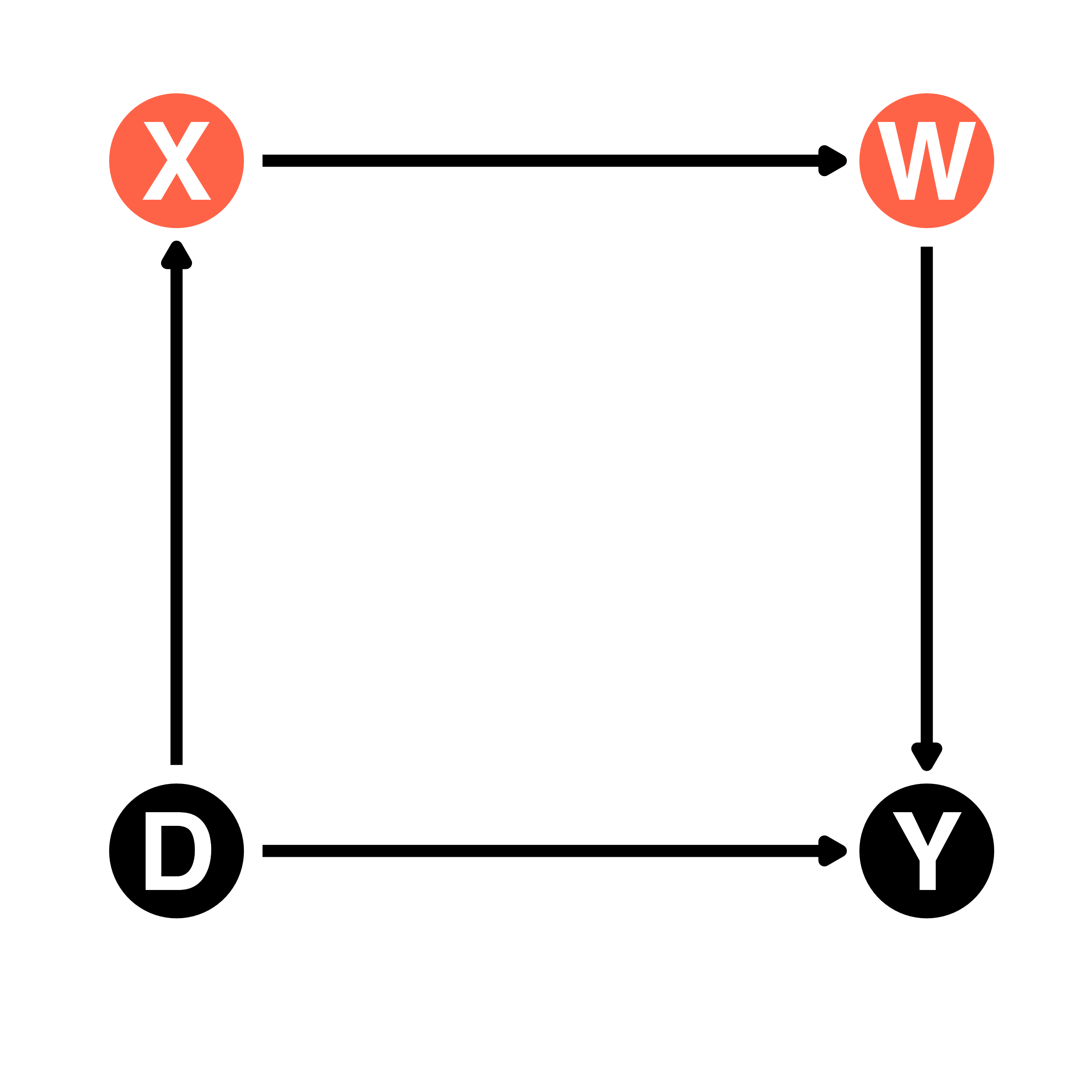
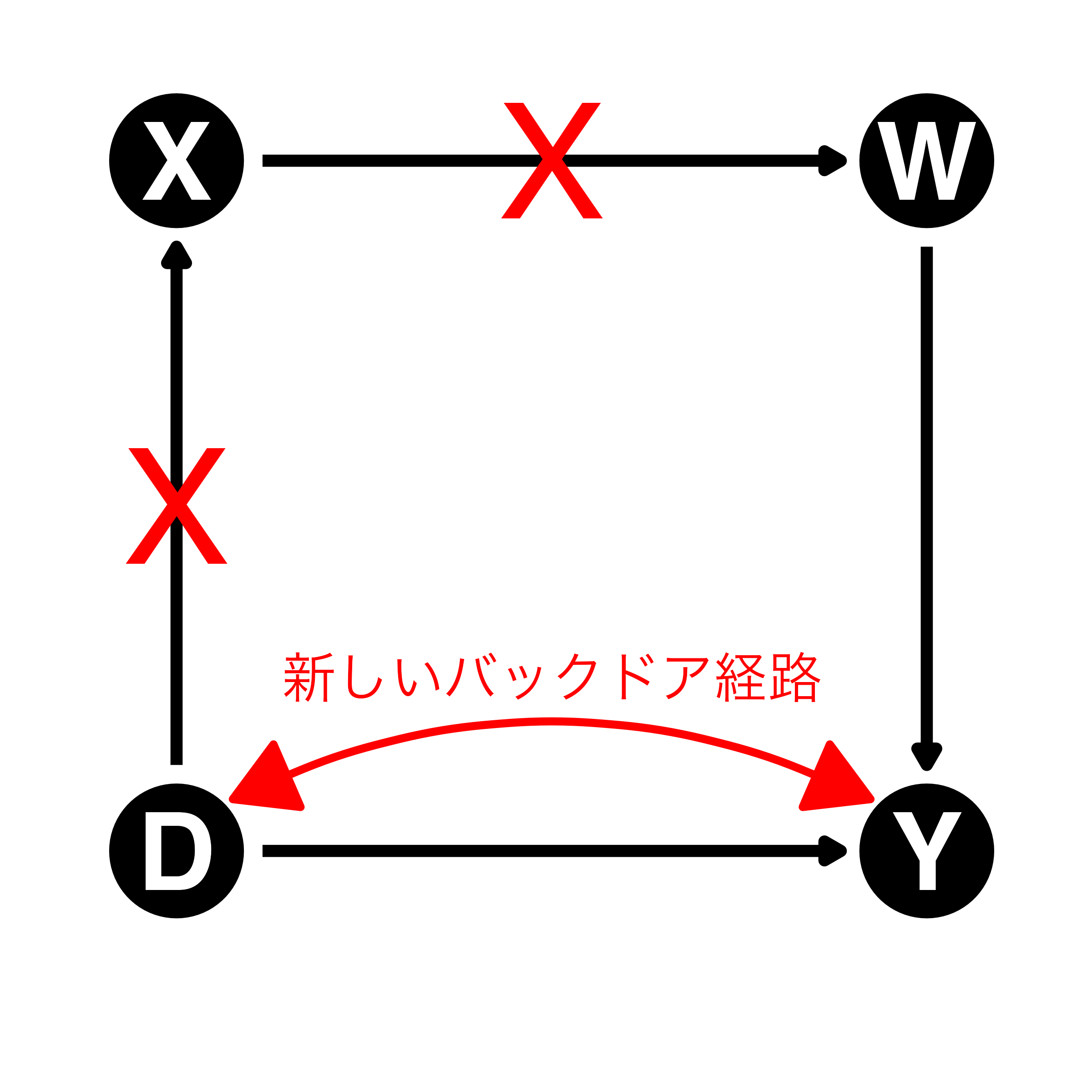
合流点、中間点はいずれも処置後変数(処置後変数バイアスの原因)
- モデルに投入すると新しいバックドア経路が開く(右はXを統制した例)
- \(\Rightarrow\) 合流点と中間点はモデルに投入しない!
- \(\Rightarrow\) 合流点はそもそも「結果の結果」だから投入しない!

応用
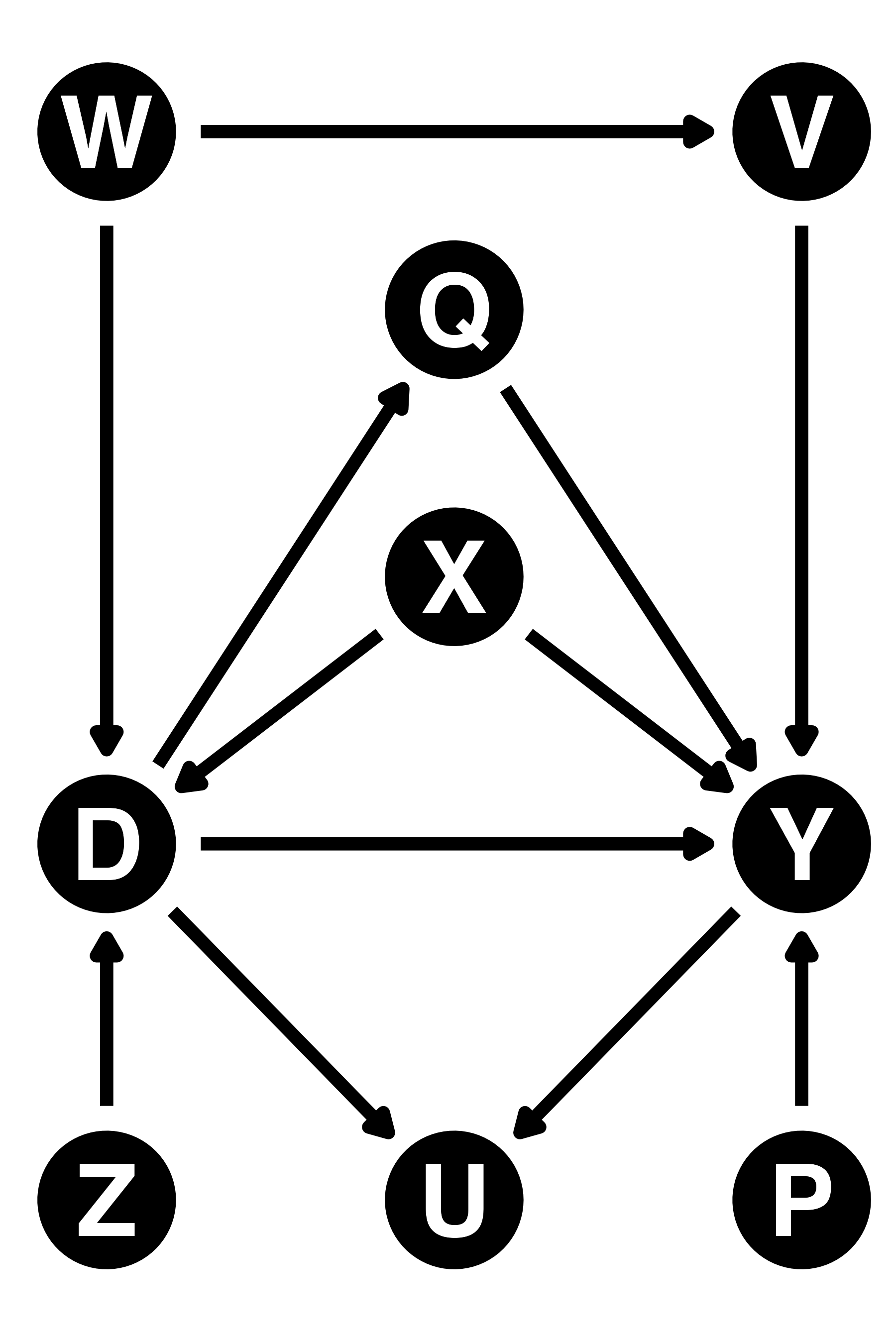
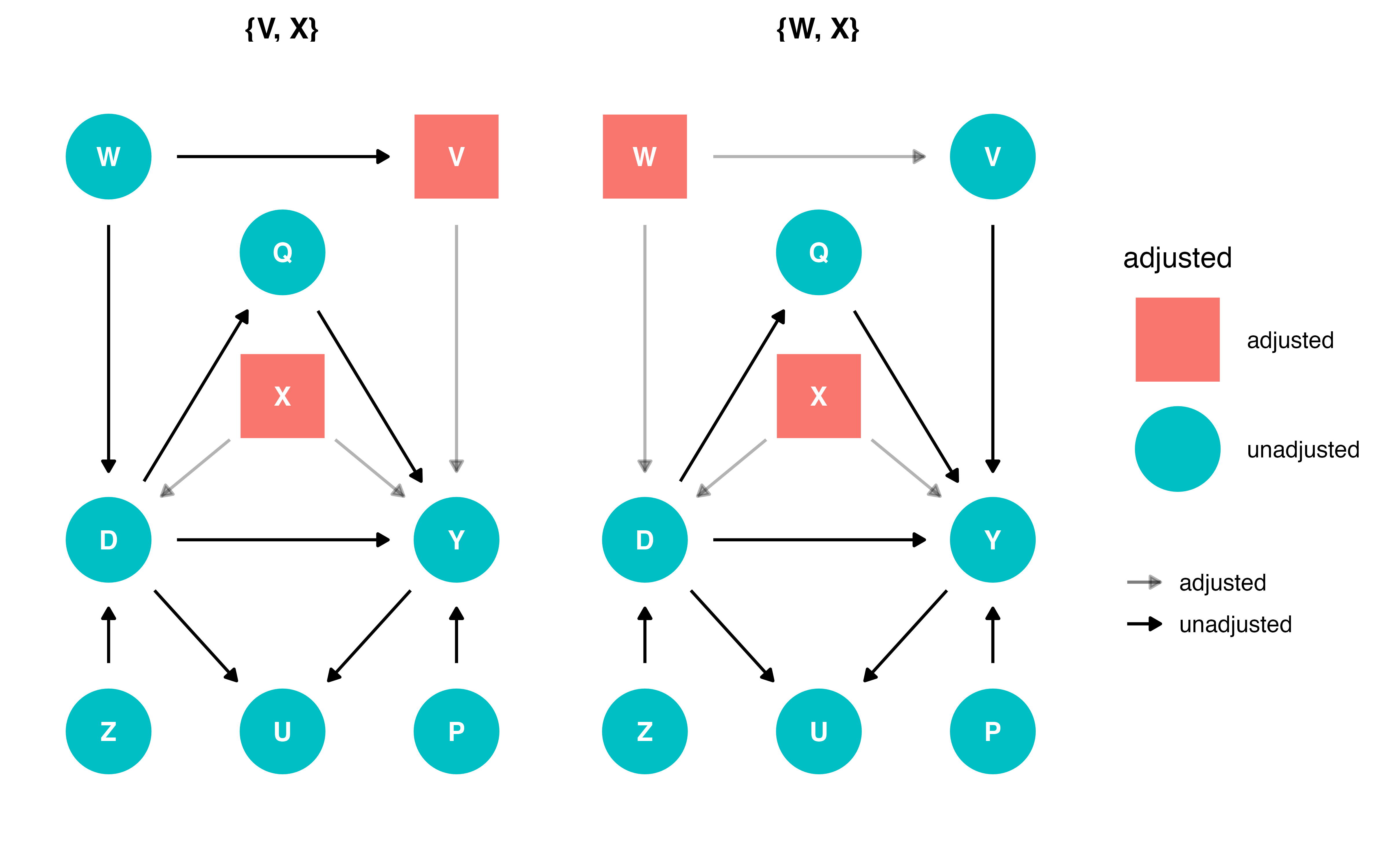
分岐点を持つバックドア経路は計2つ
- D \(\leftarrow\) W \(\rightarrow\) V \(\rightarrow\) Y
- D \(\leftarrow\) X \(\rightarrow\) Y
- 2つの経路すべてを閉じる
- {W, X}か{V, X}、{W, V, X}を統制
DAGの書き方
DAGの作成および変数選択のためのRパッケージ:{dagitty} + {ggdag}
my_dag <- dagify(
Y ~ D + V + X + P + Q,
V ~ W,
D ~ W + X + Z,
U ~ D + Y,
Q ~ D,
exposure = "D",
outcome = "Y",
coords = list(x = c("Y" = 2, "D" = 0, "W" = 0, "V" = 2, "X" = 1, "Z" = 0, "P" = 2, "U" = 1, "Q" = 1),
y = c("Y" = 0, "D" = 0, "W" = 2, "V" = 2, "X" = 0.75, "Z" = -1, "P" = -1, "U" = -1, "Q" = 1.5))
)
ggdag(my_dag)統制変数の提案
6 交互作用
交互作用とは
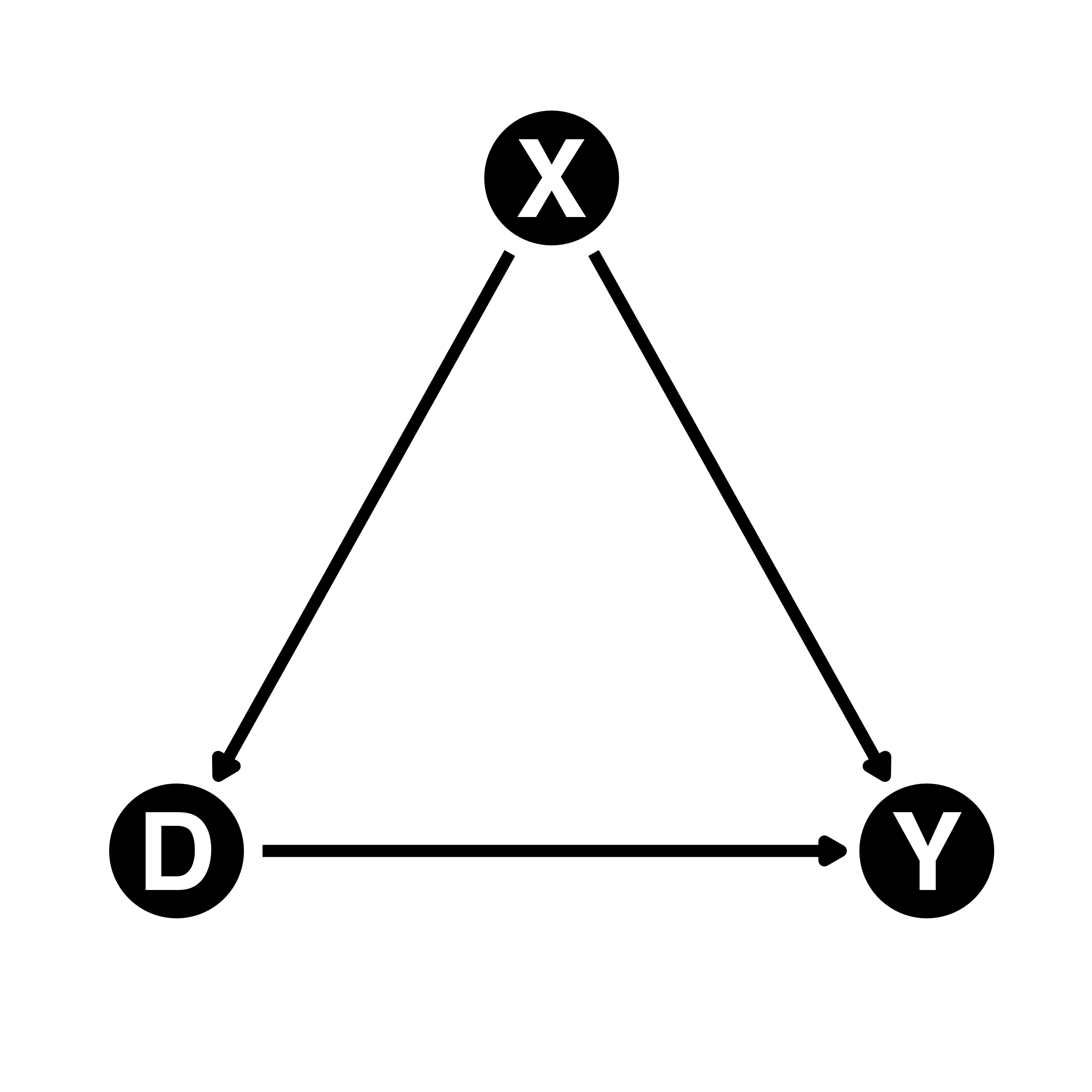
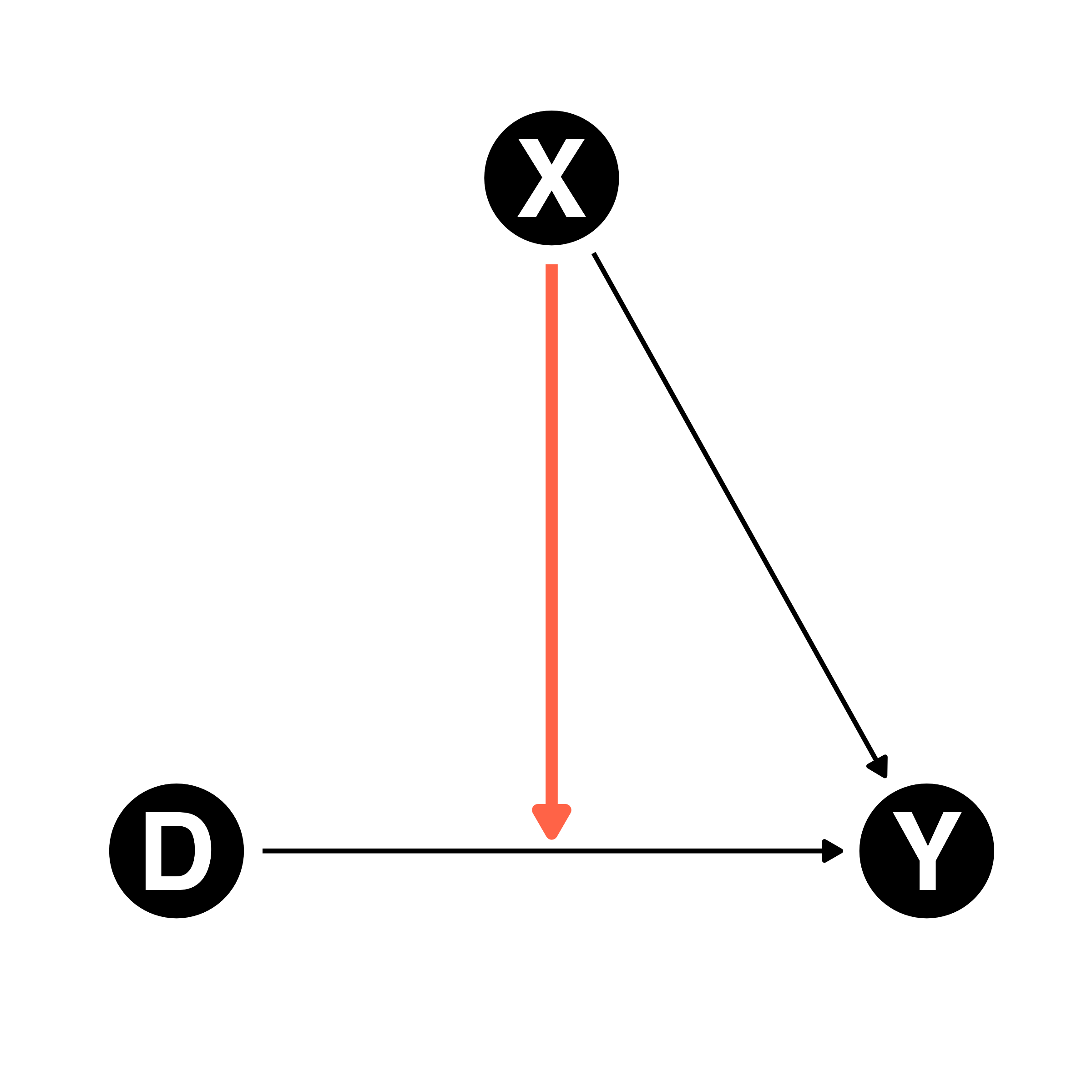
交互作用(Interaction):D \(\rightarrow\) Yの影響がXの値に依存する
- 左:Xが交絡要因・分岐点(confounder)
- 右:Xが調整変数1(mediator)
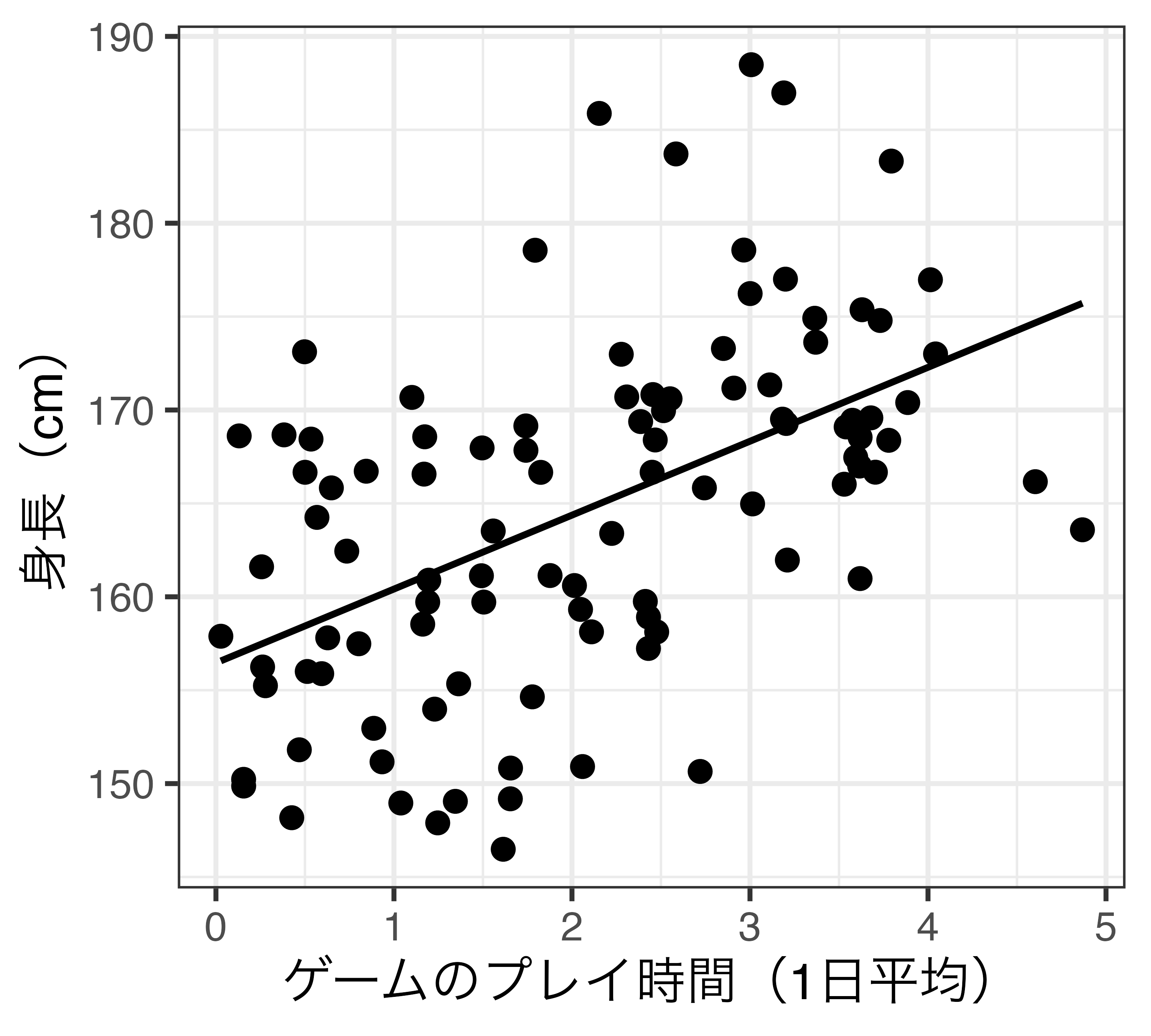
交互作用の例
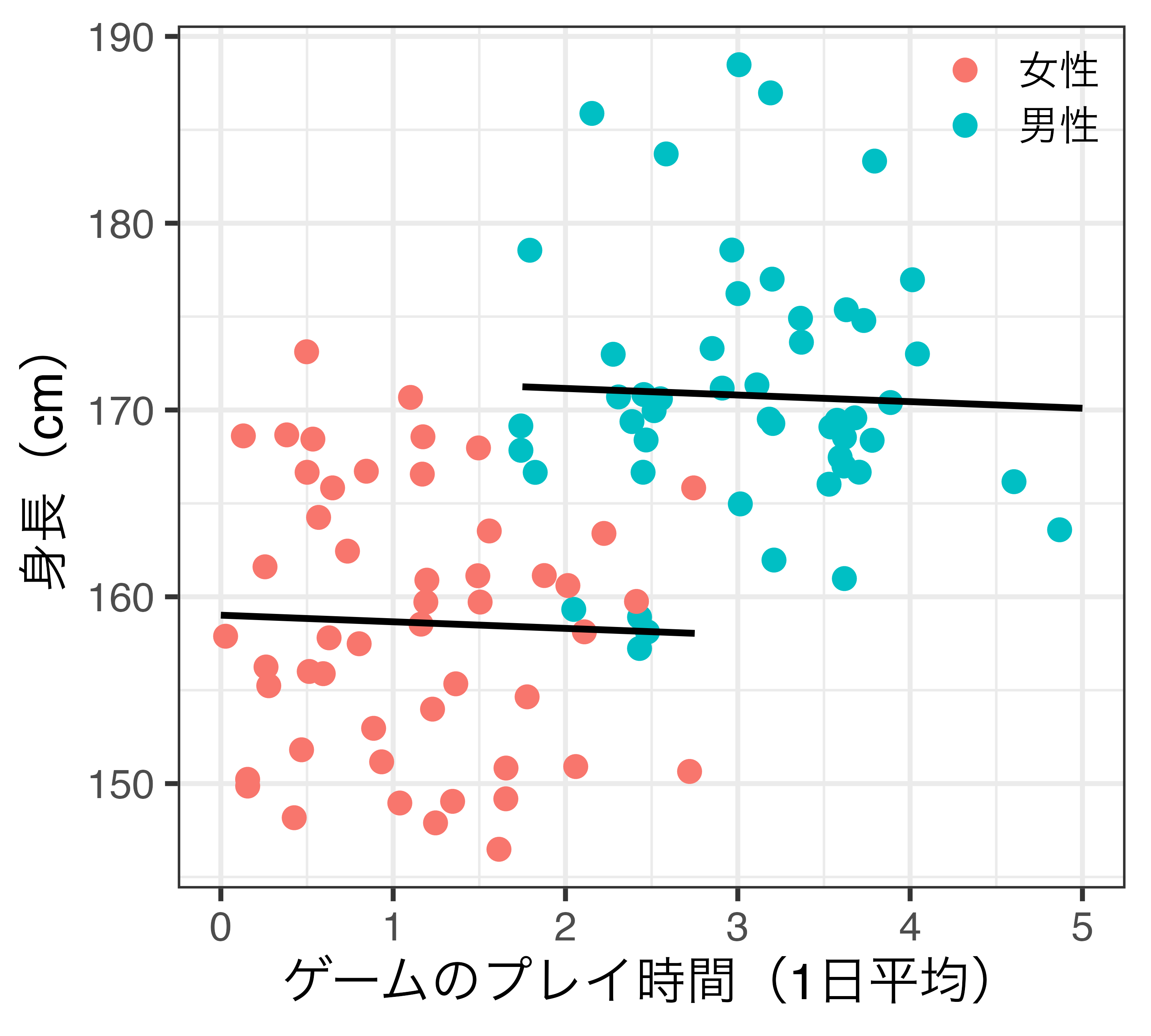
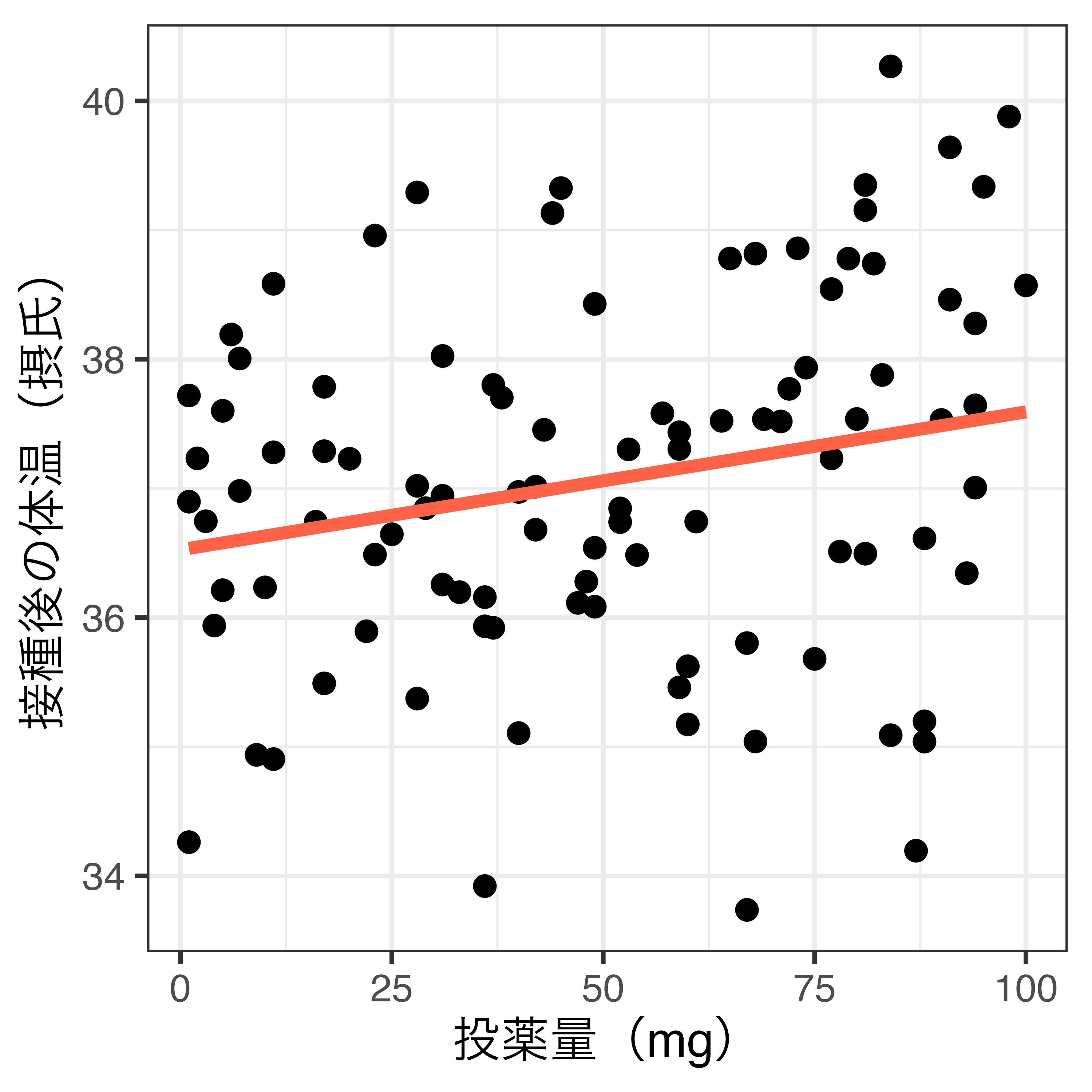
Dの処置効果がXに値によって異なる場合
- 不均一な処置効果(heterogeneous treatment effect)
- または条件付きATE(conditional average treatment effect; CATE)
- 例)薬の効き目が性別によって異なる
- 直線は単回帰分析に基づく回帰直線
交互作用のモデリング
通常の重回帰モデルに交差項(interaction term)を投入
- 交差項:2つ以上の変数の積(以下の\(D_i X_i\))
- DとXの交互作用なし:\(Y_i = \alpha + \tau D_i + \beta X_i + \varepsilon_i\)
- DとXの交互作用あり:\(Y_i = \alpha + \tau D_i + \beta X_i~ +\) \(\gamma\) \(D_i X_i\) \(+~ \varepsilon_i\)
重回帰分析との比較(図)
- 重回帰分析(左):男女の傾きが同じ
- 交互作用モデル(右):男女の傾きが異なる
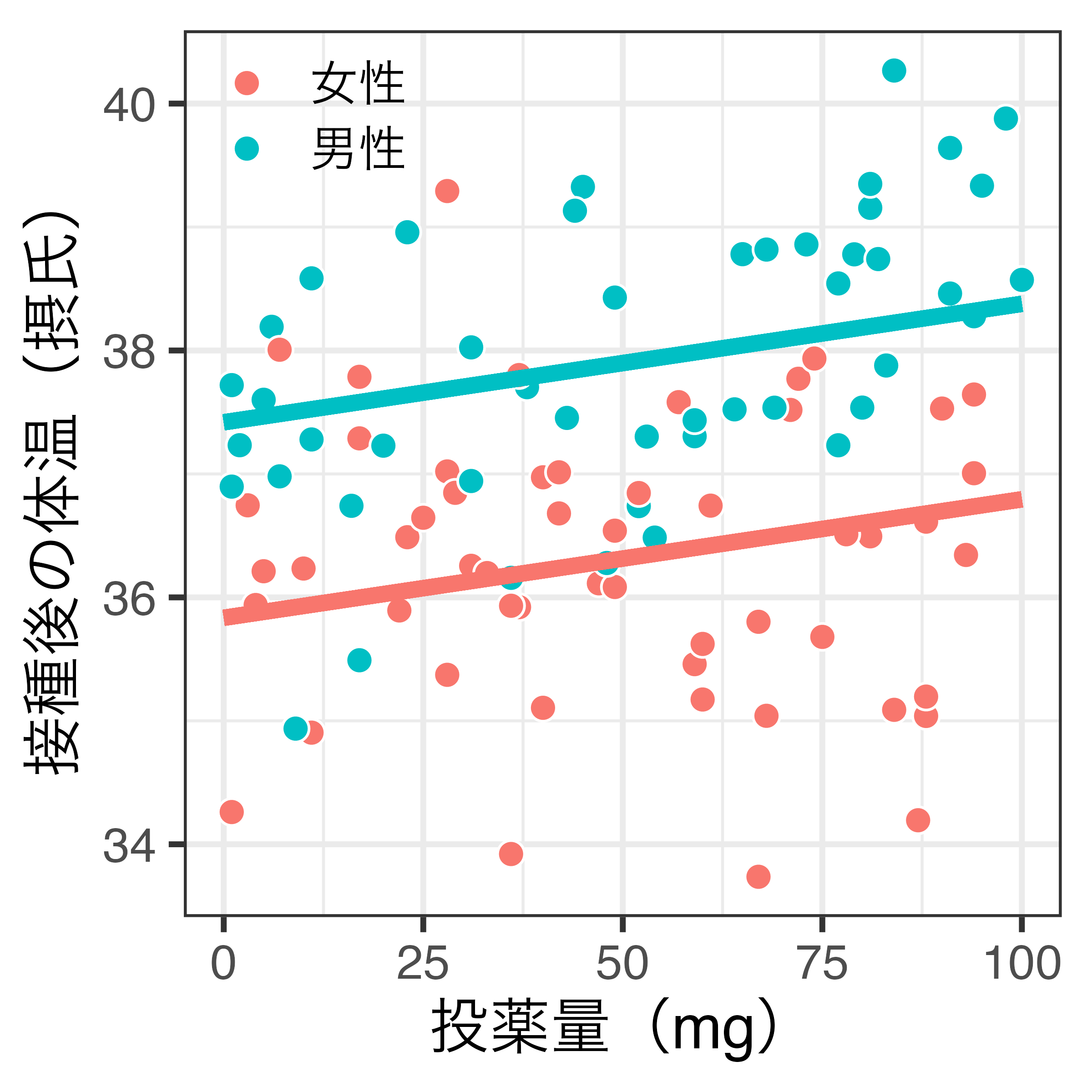
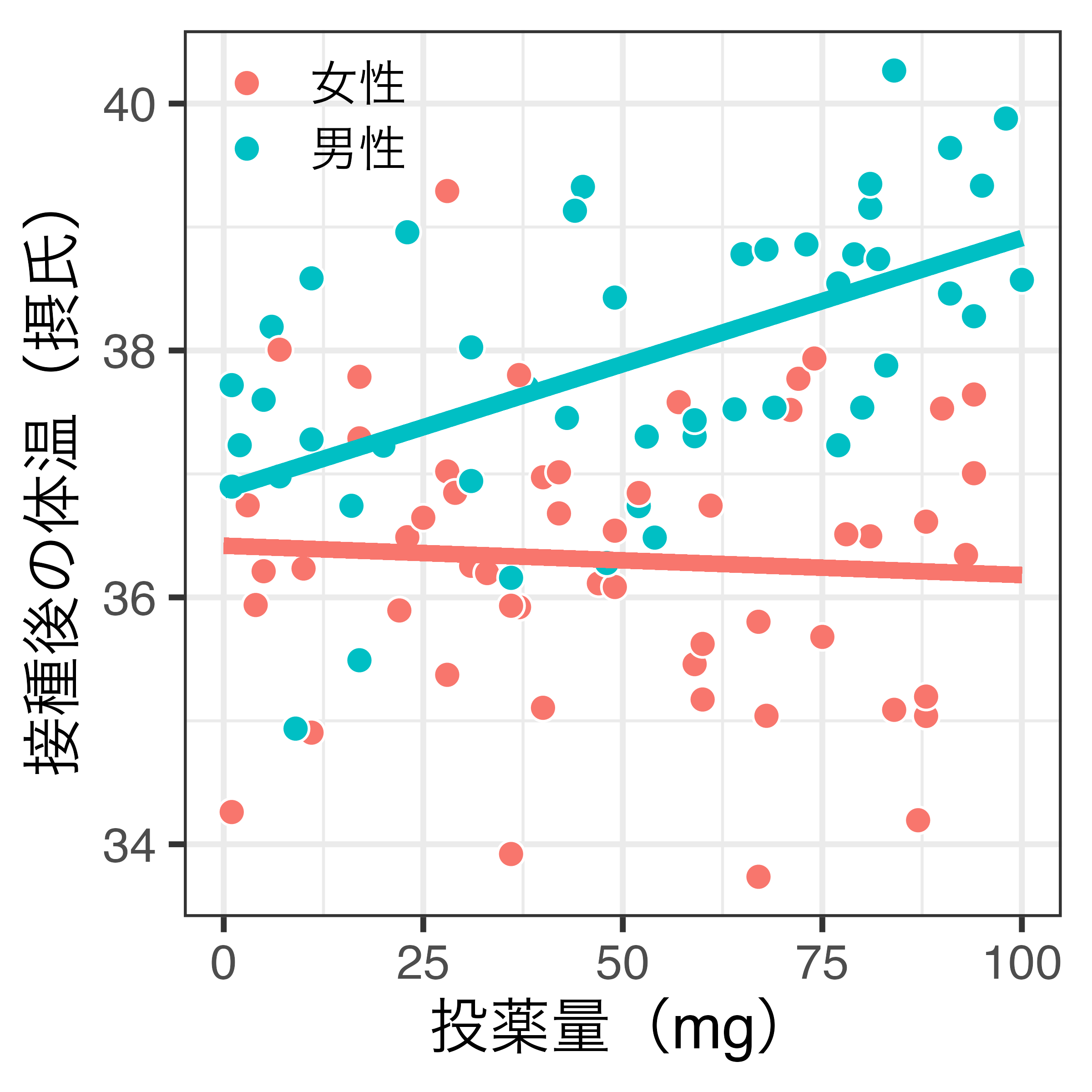
重回帰分析との比較(表)
| 交互作用なし | 交互作用あり | |
|---|---|---|
| 切片 | 35.835 (0.245) | 36.419 (0.329) |
| 投薬量 | 0.010 (0.004) | -0.002 (0.006) |
| 男性ダミー | 1.584 (0.221) | 0.442 (0.438) |
| 投薬量:男性ダミー | 0.023 (0.007) | |
| Num.Obs. | 100 | 100 |
| R2 | 0.377 | 0.436 |
| R2 Adj. | 0.365 | 0.418 |
| 注:カッコ内はHC2頑健標準誤差 | ||
- 係数の解釈:他の条件が同じであれば投薬量が1単位(= 1mg)増えると体温の期待値は0.002単位(0.002℃)下がる
- これで大丈夫?
- 何か忘れていませんか?回帰式に処置変数(投薬量)は2回登場するはず
交互作用の解釈
処置効果は\(\tau\)でなく、\(\tau + \gamma X_i\)
\[ \begin{align} Y_i & = \alpha + \tau D_i + \beta X_i + \gamma D_i X_i + \varepsilon_i \\ & = \alpha + (\tau + \gamma X_i) D_i + \beta X_i + \varepsilon_i \end{align} \]
- \(X_i = 0\)の時の処置効果、\(X_i = 1\)の時の処置効果、\(X_i = 3\)の時の処置効果、…
- 限界効果(marginal effect)
- 交互作用は予測値と限界効果に基づいて解釈すべき(回帰係数にこだわらない)
- 詳細はBrambor(2006)を参照
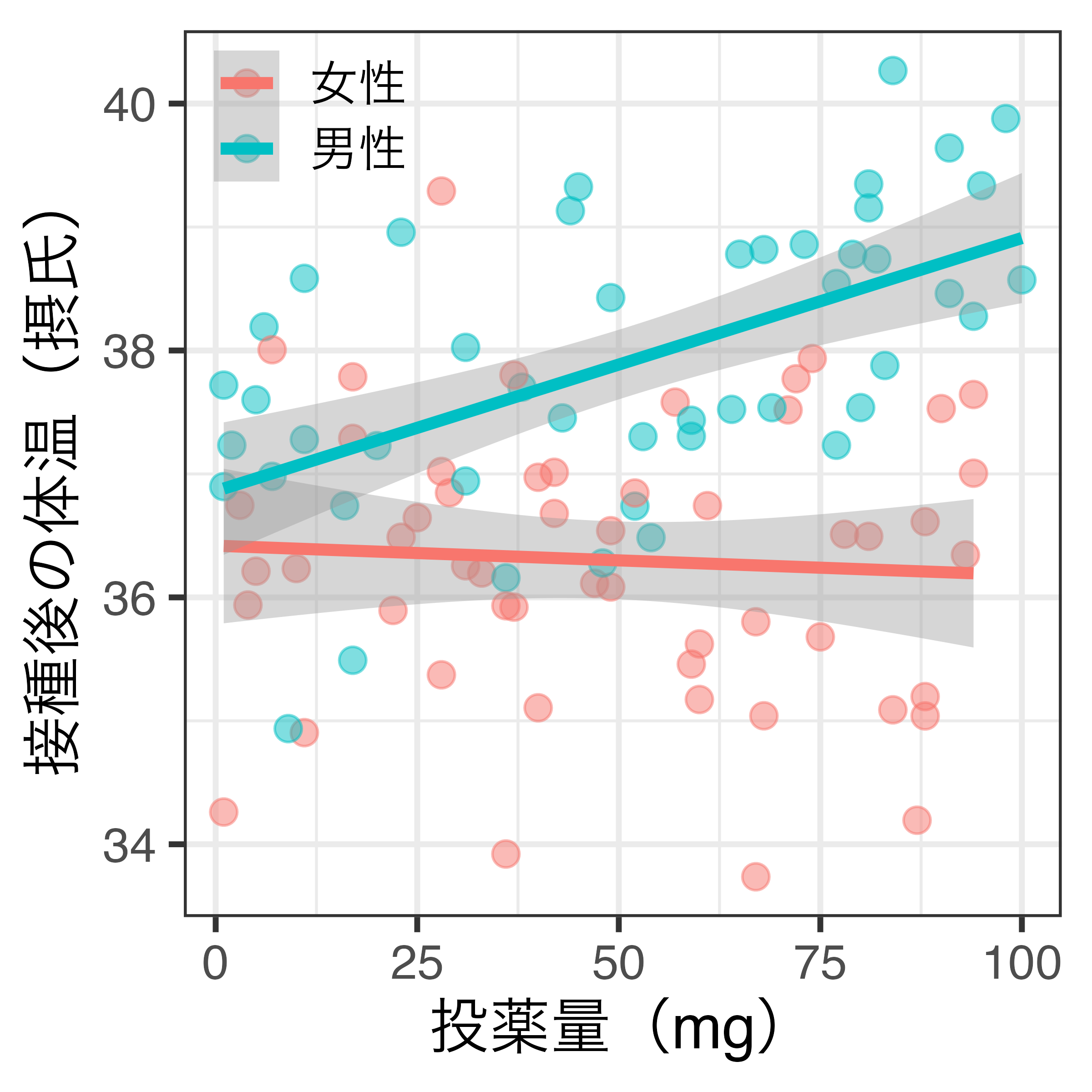
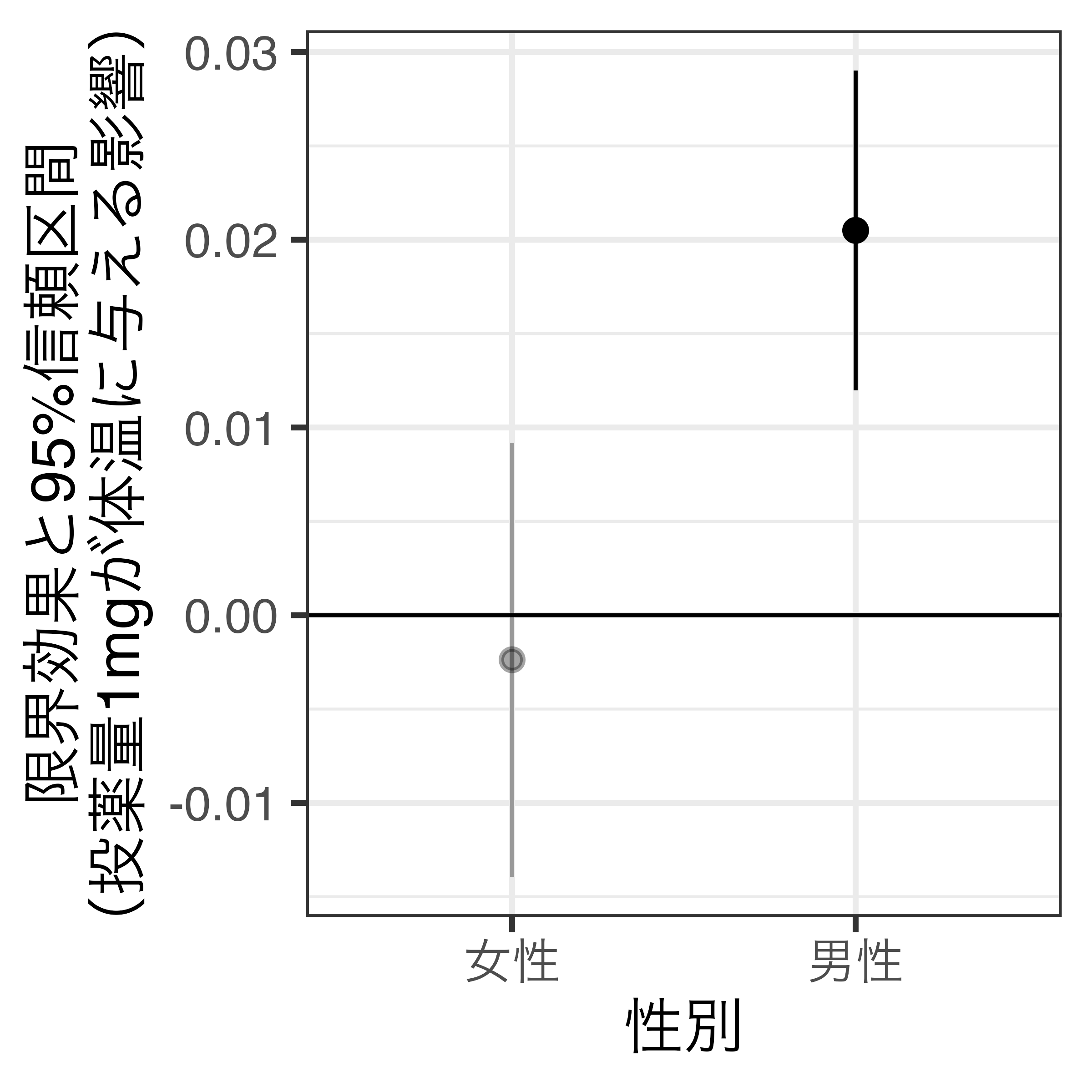
予測値(左)と限界効果(右)
男性の場合、投薬量が1mg増えると体温は約0.02℃上がる。一方、女性の場合、統計的有意な処置効果は確認できない1。
7 実装
推定
共通
- 予測値、効果量を示すことで実質科学的な議論を
- 交差項を含むモデルの場合、限界効果も示すこと
実験データの場合
- 処置変数は外生変数(の可能性が非常に高い)であるため、統制変数は不要
- 実験でも処置の自己選択が生じるケースもあるため、統制変数が必要な場合も
- 統制変数を入れても良い
- 標準誤差が小さくなる
- 処置後変数は投入しない!
観察データの場合
- 処置変数は内生変数(の可能性が非常に高い)であるため、統制変数が必要
- 慎重な変数選択が必要
実験データと重回帰分析
- Freedman(2008a, 2008b)の問題提起
- 内生性の問題が多く解決されているはずの実験データであっても、共変量調整は場合によって精度の低下、バイアスの導入、信頼できない標準誤差の原因になる
- Lin(2013)の提案
- Freedmanの議論は正しいが、以下の2つを採用することで解決可能(大標本を前提とする)
- 処置変数と共変量間の交差項を投入(共変量が複数ならすべての共変量との交差項を投入)
- 頑健標準誤差(Huber–White sandwich standard error)を使用
効果量
処置効果の大きさを数値化し、評価する(ドメイン知識が必要)
- 統制群と処置群間の結果変数の差
- 差はいくらか、または何SD分かなど
- 処置変数が連続の場合は、最小値 \(\rightarrow\) 最大値、平均を中心とした \(\pm\) 1 or 2SDなど
心理学を中心とした効果量の議論
- Standardized mean difference
- Cohen’s d
効果量の例:Cohen’s d
幅広く使われる効果量(Cohen 1980)
- \(s_{\cdot}^2\)は不偏分散
\[ \begin{align} d & = \frac{\bar{x}_1 - \bar{x}_2}{s} \\ s & = \sqrt{\frac{(n_1 - 1)s_1^2 + (n_2 - 1)s_2^2}{n_1 + n_2 - 2}} \end{align} \]
Cohen(1980)の基準(すべての学問分野に適用される基準ではない)
- 小さい効果量:d = 0.2
- 中程度の効果量:d = 0.5
- 大きい効果量:d = 0.8
統制変数の解釈について
基本的に統制変数の係数は解釈しない
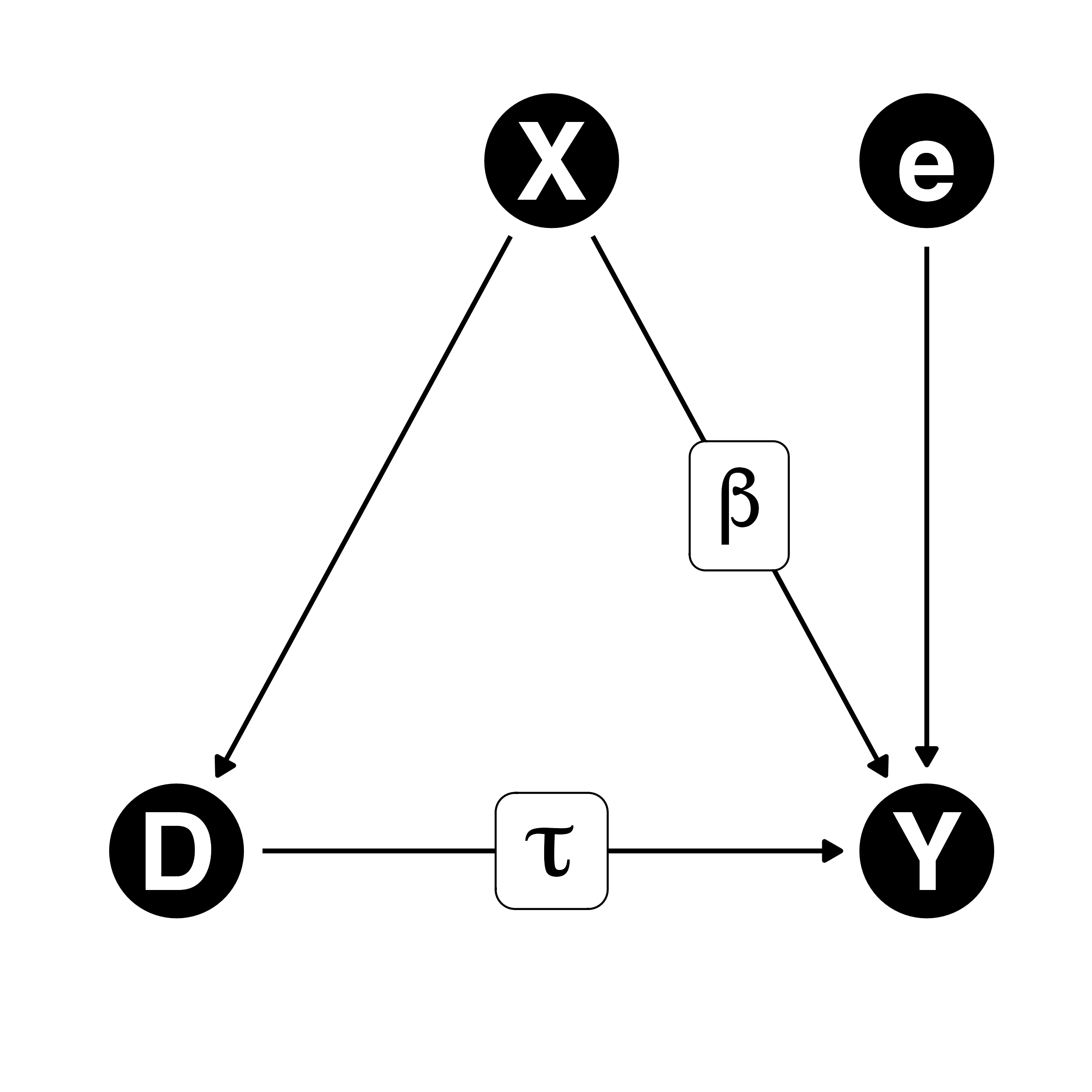
信頼できる\(\tau\)を推定するために、交絡要因(分岐点)であるXを統制
- \(\tau\):DがYに与える効果
- \(\beta\):XがYに与える効果?
- X \(\rightarrow\) Yの関係においてDは中間点(媒介変数)
- 中間点は統制しないのが原則
- XがYに与える効果を推定するためにはモデルからDを除外すべき
回帰分析